1.量子コンピューターで誤り訂正機能を実現(2/2)まとめ
・Sycamoreデバイスはリセットプロトコルのおかげでエラーを蓄積せずにエラー修正を実行可能
・反復コードを使用してエラーの指数関数的抑制も達成出来る事が検証できた
・本実験は、QECシステムのこれまでで最大のストレステストであったが目標は達成できた
2.量子エラー訂正で実証できた事
以下、ai.googleblog.comより「Demonstrating the Fundamentals of Quantum Error Correction」の意訳です。元記事は2021年8月11日、Jimmy ChenさんとMatt McEwenさんによる投稿です。
アイキャッチ画像のクレジットはPhoto by JuniperPhoton on Unsplash
指数関数的なエラー抑制
相関エラーの重要な原因であるリークを軽減したので、次に、量子ビット数を増やしたときに、反復コード(repetition codes)が予測される指数関数的なエラーの減少をもたらすかどうかをテストしました。
反復コードを実行するたびに、検出したエラーのコレクションが生成されます。検出したエラーは個々の量子ビットではなく量子ビットのペアにリンクされているため、エラーが発生した場所をつなぎ合わせるために、全ての検出を調べる必要があります。
この作業は、デコードと呼ばれる手順です。エラーをデコードすると、データ量子ビットに適用する必要がある修正が何かわかります。ただし、使用されるデータ量子ビットの数に対してエラー検出が多すぎると、デコードが失敗し、論理エラーが発生する可能性があります。
反復コードをテストするために、5~21量子ビットの範囲のサイズのコードを実行し、エラー訂正ラウンドの数も変更します。また、さまざまな種類の量子エラーに敏感な2種類の反復コード(位相反転コードまたはビット反転コード)を実行します。ラウンド数の関数として論理エラー確率を見つけることにより、各コードサイズとコードタイプの論理エラー率を適合させることができます。私たちのデータでは、コードサイズが大きくなると、論理エラー率が実際に指数関数的に抑制されることがわかります。
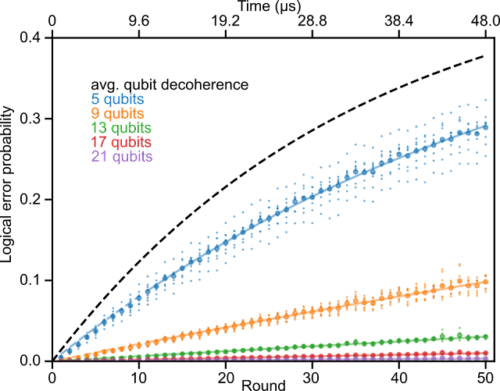
デコード後に論理エラーが発生する確率と実行されたラウンド数
さまざまなサイズの位相反転反復コード(phase-flip repetition code)について示されています
エラー抑制は、エラースケーリングパラメーターLambda(Λ)を使用して定量化できます。ここで、Lambda値が2の場合、反復コードに4つのデータ量子ビットを追加するたびに論理エラー率が半分になります。
私たちの実験では、位相反転コードで3.18、ビット反転コードで2.99のラムダ値となる事を発見しました。これらの実験値を、相関エラーのない単純なエラーモデルに基づいて、予想されるラムダの数値シミュレーションと比較できます。これによると、ビット反転コードと位相反転コードの値がそれぞれ3.34と3.78になります。
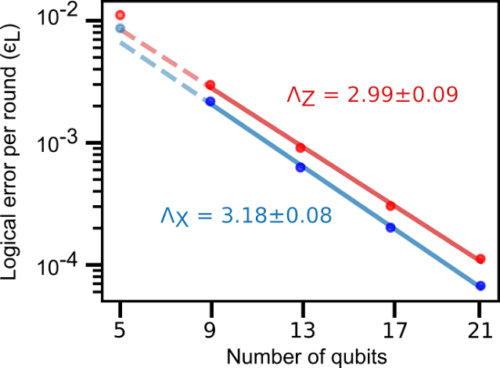
位相反転(X)およびビット反転(Z)反復コードのラウンドあたりの論理エラー率と量子ビット数の関係
線は指数関数的減衰の適合を示し、Λは指数関数的減衰のスケールファクターです。
複数ラウンドのエラー検出を実行しながら、Lambdaが任意のプラットフォームで測定されたのはこの実験が初めてです。ラムダの実験値とシミュレーション値がどれほど近いかについては特に興奮しています。これは、予期しないエラーが多く発生することなく、非常に単純なエラーモデルでシステムを記述できることを意味します。
それにもかかわらず、合意(the agreement)は完全ではなく、相関エラーの追加の原因を含め、QECアーキテクチャの非理想性を理解するために行われるべきさらなる研究があることを示しています。
次に何をすべきか?
本研究は、量子エラー訂正(QEC:Quantum Error Correction)の2つの重要な前提条件を示しています。1つは、Sycamoreデバイスが、新しいリセットプロトコルのおかげで、時間の経過とともにエラーを蓄積することなく、エラー修正を何度も実行できることです。
2つ目は、反復コードを使用してエラーの指数関数的抑制が達成出来る事を示すことにより、QEC理論とエラーモデルを検証することができました。
これらの実験は、QECシステムのこれまでで最大のストレステストであり、最大のテストでは1000の絡み合いゲート(entangling gates)と500の量子ビット測定を使用しました。これらの実験から学んだことを、私達の目標とするQECアーキテクチャである「2Dサーフェスコード(2D surface code)」に適用することを楽しみにしています。
2D surface codeでは、さらに優れたパフォーマンスでさらに多くの量子ビットが必要になります。
3.量子コンピューターで誤り訂正機能を実現(2/2)関連リンク
1)ai.googleblog.com
Demonstrating the Fundamentals of Quantum Error Correction
2)www.nature.com
Removing leakage-induced correlated errors in superconducting quantum error correction
Exponential suppression of bit or phase errors with cyclic error correction



