量子コンピュータを使った量子材料シミュレーションで高精度を達成

１．量子コンピュータを使った量子材料シミュレーションで高精度を達成まとめ

・量子プロセッサは古典的なアプローチでは計算が難しいタスクを解ける可能性を持つ
・本気の競争相手と見なされるために古典的手法を超える計算精度を見せる必要があった
・フーリエ変換を利用し材料シミュレーションで前例のないレベルの精度を達成できた

２．量子コンピュータを使った最新の精度

以下、ai.googleblog.comより「Achieving Precision in Quantum Material Simulations」の意訳です。元記事の投稿は2021年6月25日、Charles NeillさんとZhang Jiangさんによる投稿です。

アイキャッチ画像のクレジットはPhoto by Nejc Soklič on Unsplash

2019年の秋に、私たちは、Sycamore 量子プロセッサ用にあつらえたオーダーメイドの問題を実行したときに、最も強力な古典的コンピューターよりも優れた性能を発揮できることを実証しました。

次の課題は、この結果を拡張して、材料科学、化学、物理学における実務的な問題を解決することです。しかし、これらの問題に対して従来のコンピューターの能力を超えることは困難であり、最先端の精度を達成するために新しい洞察が必要になります。このような物理的問題の量子シミュレーションを実行することの一般的な難しさは、量子粒子の波の性質に根ざしており、初期設定の偏差、環境からの干渉、または計算の小さなエラーが計算結果の大きな偏差につながる可能性があります。

もうすぐ発表される今後の2つの出版物では、量子材料のシミュレーションタスクで記録的なレベルの精度を達成するための青写真の概要を説明します。最初の研究では、細いワイヤーなどの1次元システムを検討し、電流やコンダクタンスなどの電子特性を正確に計算する方法を示します。

2番目の研究では、重要な物理的特性をシミュレートするために、相互作用する電子を記述するフェルミハバードモデル(Fermi-Hubbard model)を量子プロセッサにマッピングする方法を示します。これらの研究は、バッテリーや医薬品などの実用的なアプリケーションでより複雑なシステムをシミュレートするという長期的な目標の実現に向けて重要な一歩を踏み出しました。

メンテナンス中の量子希釈冷凍機の1つの底面図
動作中、この画像内に浮かんでいるマイクロ波ワイヤは、量子プロセッサ、たとえばSycamoreチップに接続され、最下段の温度を絶対零度より数十ミリ度高くします。

量子材料の電子特性の計算

Natureに掲載される論文「Accurately computing electronic properties of a quantum ring」では、量子材料の主要な電子特性を再構築する方法を紹介します。

この研究の焦点は、1次元の導体にあります。非常に細いワイヤを模倣するために、Sycamoreプロセッサで18量子ビットからループを形成することによってシミュレートします。

一連の簡単な教科書的実験を通して、基礎となる物理学を説明します。このワイヤーの「バンド構造(band-structure)」の計算から始めます。バンド構造は、金属内の電子のエネルギーと運動量の関係を表します。

このような構造を理解することは、電流や電流の流れやすさ(conductance)などの電子特性を計算する上で重要なステップです。1,400を超える論理演算で構成される18量子ビットのアルゴリズムであり、短期的なデバイスにとって重要な計算タスクであるにもかかわらず、1%という低い合計エラーを達成することができます。

このレベルの精度を可能にする重要な洞察は、フーリエ変換の堅牢な特性に由来します。私たちが測定する量子信号は、少数の周波数で時間とともに振動します。この信号をフーリエ変換すると、発振周波数(この場合はワイヤ内の電子のエネルギー)にピークが現れます。

実験的な欠陥は観測されたピークの高さ(振動の強さに対応)に影響しますが、中心周波数はこれらのエラーに対して堅牢です。一方、中心周波数は、私たちが研究したいワイヤーの物理的特性(たとえば、電子が感じる局所電場の小さな障害を明らかにする)に特に敏感です。私たちの研究の本質は、フーリエ領域で量子信号を研究することで、基礎となる量子システムの高感度プローブを提供しながら、実験エラーに対する堅牢な保護を可能にすることです。

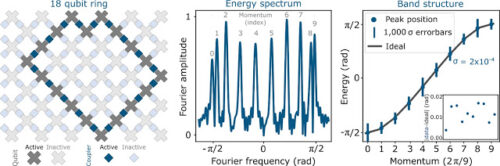
(左)54量子ビットの量子プロセッサ、シカモアの概略図。量子ビットは灰色の十字で示され、調整可能なカプラーは青い四角で示されます。18個の量子ビットが分離されてリングを形成します。
(中央)測定された量子信号のフーリエ変換。フーリエスペクトルのピークは、リング内の電子のエネルギーに対応します。各ピークは、固定された運動量を持つ進行波に関連付けることができます。(右)各ピークの中心周波数(ワイヤ内の電子のエネルギーに対応)が、ピークインデックス(運動量に対応)に対してプロットされます。エネルギーと運動量の間の測定された関係は、量子ワイヤーの「バンド構造」と呼ばれ、電流や電流の流れやすさなどの材料の電子特性に関する貴重な情報を提供します。

フェルミハバードモデルの量子シミュレーション

論文「Observation of separated dynamics of charge and spin in the Fermi-Hubbard model」では、相互作用する電子の動きに焦点を当てています。

粒子間の相互作用は、高温超伝導やスピン電荷分離などの新しい現象を引き起こします。この振る舞いを捉える最も単純なモデルは、フェルミハバードモデル(Fermi-Hubbard model)として知られています。

金属などの材料では、原子核が結晶格子を形成し、電子が格子サイトから格子サイトにホップして電流を運びます。これらのシステムを正確にモデル化するには、電子が互いに近づくときに感じる反発力を含める必要があります。Fermi-Hubbardモデルは、ホッピング速度(J)と反発強度(U)を表す2つの単純なパラメーターを使用してこの物理学を捕捉します。

このモデルの動きは、2つの物理パラメータをプロセッサの量子ビットの論理演算に割り当てることで実現します。これらの操作を使用して、電子の電荷とスピン密度の両方が量子ビット配列の中心近くでピークに達する電子の状態をシミュレートします。システムが進化するにつれて、電子間の強い相関関係により、電荷密度とスピン密度が異なる速度で広がります。私たちの結果は、相互作用する電子の直感的な絵面を提供し、超伝導量子ビットを持つ量子材料をシミュレートするためのベンチマークとして機能します。

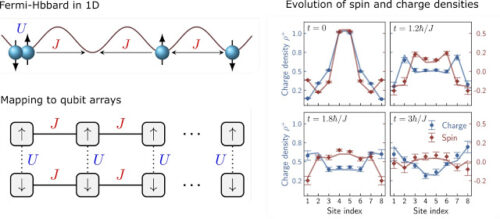
左上図：周期ポテンシャルにおける1次元Fermi-Hubbardモデルの図。電子は青色で示され、スピンは接続された矢印で示されます。電位場の谷間の距離であるJは、「ホッピング」速度、つまり、電子が電位内のある谷から別の谷に遷移する速度を反映し、振幅であるUは、電子間の反発の強さを表します。左下図：量子ビットラダーでのモデルのシミュレーション。各量子ビット(正方形)は、スピンアップまたはスピンダウン(矢印)を伴うフェルミ粒子状態を表します。
右図：モデルの時間発展は、電荷とスピンの分離した拡散速度を明らかにします。点と実線は、それぞれ実験結果と数値の正確な結果を表しています。t = 0で、電荷密度とスピン密度は中央のサイトでピークになります。その後、電荷密度は広がり、スピン密度よりも速く境界に到達します。

結論

量子プロセッサは、古典的なアプローチの能力を超える計算が難しいタスクを解決する可能性を秘めています。ただし、これらの設計された量子プラットフォームが本気の競争相手と見なされるためには、現在の最先端の古典的な方法を超える計算精度を提供する必要があります。最初の実験では、単純な材料シミュレーションで前例のないレベルの精度を示し、2番目の実験では、相互作用する電子の現実的なモデルを量子プロセッサに埋め込む方法を示します。これらの実験結果が、古典的なコンピューティングの地平を超えて進むという目標を前進させるのに役立つことを願っています。