Duality：強化学習への新しいアプローチ

１．Duality：強化学習の新しいアプローチまとめ

・既存の強化学習手法であるQ-learningやactor-criticなどは計算が大変な部分は近似値を使っている
・双対性を利用する事により、近似が不要なもっとすっきりとした式に変換する事が出来る
・新しい双対ベースの実装は、actor-critic法と比較して大幅に高い性能を実現できる

２．Duality-Based Solutionとは？

以下、ai.googleblog.comより「Duality — A New Approach to Reinforcement Learning」の意訳です。元記事の投稿は2020年7月8日、Ofir NachumさんとBo Daiさんによる投稿です。

既存の強化学習手法であるQ-learningやactor-criticなどは、計算が大変な部分は近似値を使っているのですが、Duality、数学用語で双対性(1つの対象に対し2つの等価な記述法が存在する事)を利用する事により、近似が不要なもっとすっきりとした式に変換する事が出来、その結果、性能もアップするという、これまたあったまイイなぁ、と思えるお話です。

数学っぽく、Dualityっぽく、convexっぽいアイキャッチ画像のクレジットはPhoto by Bekky Bekks on Unsplash

強化学習(RL:Reinforcement Learning)は、複雑な環境でエージェントに目標を達成させるために、一連の意思決定を行えるようにする際に使用される一般的なアプローチです。

例えば、エージェントがロボットの関節モーターを制御して目標の場所への経路を探すロボット操作や、エージェントに最短でテレビゲームを解く事を求めるゲームプレイなどがあります。

Q-learningやactor-criticなど、最近成功した多くのRLアルゴリズムは、RL問題を制約充足問題(constraint-satisfaction problem、複数の制約条件を満たす物体や状態を見つけるという数学的問題)として扱う事を提案しています。

この場合、環境の全ての「状態」に制約が存在する事になります。例えば、視覚ベースのロボット操作の環境の「状態」とはカメラ入力の全パターンに該当します。

制約充足アプローチが実際に広く普及しているにもかかわらず、この戦略は、現実世界の環境の複雑さにより実現が難しいことがよくあります。

現実世界のシナリオ(ロボット操作の例など)では、「状態」が非常に多様であり、場合によっては数え切れないほどです。このようなケースでは、どうすれば任意の入力に関連付けられた膨大な数の制約を満たすことを学習できるでしょうか？

Q-learningとactor-criticの実装では、これらの数学的問題を無視するか、一連の大まかな近似によってそれらを曖昧にすることがよくあります。その結果、これらのアルゴリズムの実際の実装とその数学的基礎理論との間に明確な違いが生じます。

論文「Reinforcement Learning via Fenchel-Rockafellar Duality」では、私達は、RLへの新しいアプローチを開発しました。このアプローチは、現実世界の問題に役立ち、数学的原理にも忠実なアルゴリズムを実装する事を可能にします。

つまり、提案されたアルゴリズムは、それらの数学的基礎を実際の実装に変換するために非常に粗い近似を使用する事を避けます。

このアプローチは凸面双対性(convex duality)に基づいています。凸面双対性は、1つの形式で表現された問題を、より計算しやすい別の形式の同等の問題に変換するために使用される、よく研究された数学的ツールです。私達のケースでは、RLに双対性を適用して従来の制約充足問題の数学的形式を非制約の、従ってより実用的な数学問題に変換する特定の手法を開発します。

双対性に基づく解決策
双対性に基づくアプローチは、強化学習問題を数々の制約(潜在的に無限に存在する制約)とともに数学的な問題として定式化することから始まります。

この数学的問題に双対性を適用すると、同じ問題の異なる定式化が得られます。

まだ、この変換した定式化は元と同じ問題、すなわち「単一の目的に多数の制約」を持っていますが、目的と制約の内容は変更されています。

次のステップが、双対性ベースの解法の鍵です。問題を平滑化し、解決を容易にする方法として最適化でよく使用される方法である凸正則化(convex regularizer)を使用して、双対目標を保持します。

正則化関数の選択は最終ステップに重要です。そこでは、もう一度双対性を適用して、同じ問題に別の定式化をします。

今回のケースでは、fダイバージェンス正則化(f-divergence regularizer)を行います。これにより、最終的に制約のない定式化が得られます。

凸型正則化器には他の選択肢もありますが、制約のない問題を生成するには、fダイバージェンスによる正則化が比類なく望まれます。fダイバージェンスは特に、ポリシー外またはオフラインでの学習を必要とする実際的で現実的な設定での最適化に適しています。

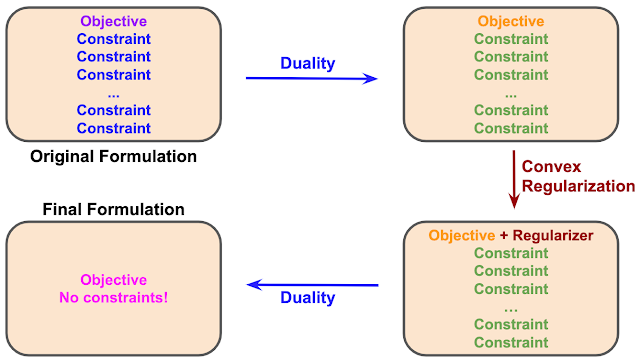
特に多くの場合、双対ベースのアプローチで規定されている双対性と正則化は、元の解の最適性を変更しません。つまり、問題の形は変わっても、解は変わっていないのです。このようにして、新しい定式化で得られた結果は、元の問題と同じ結果になりますが、はるかに簡単な方法で解く事ができます。

実験的評価
新しいアプローチのテストとして、ナビゲーションエージェントに双対性ベースのトレーニングを実装しました。エージェントはマルチルームマップの1つの角部屋からスタートし、反対側の角部屋に移動する必要があります。この条件でアルゴリズムをactor-criticベースのアプローチと比較します。

これらのアルゴリズムはどちらも同じ基礎となる数学的問題に基づいていますが、actor-criticは多数の制約を満たすことができないため、多くの近似を使用しています。対照的に、2つのアルゴリズムのパフォーマンスを比較することでわかるように、双対ベースのアルゴリズムは実際の実装により適しています。

以下の図では、学習済みエージェントによって達成された平均報酬を、各アルゴリズムのトレーニングの反復回数に対してグラフ化しています。双対ベースの実装は、actor-critic法と比較して大幅に高い報酬を実現します。

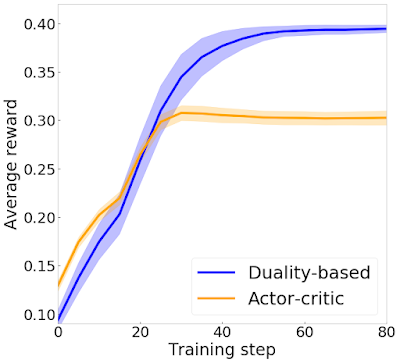
標準的なactor-critic(オレンジ)を使用するエージェントと双対ベースのアプローチ(青)を使用するエージェントによって達成される平均報酬の比較図
私達のアプローチは、より数学的な原理に加えて、より実用的な結果をもたらします。