1.集積カプセルオートエンコーダー(1/6)まとめ
・脳が備えている自己教師と帰納的バイアスのお蔭で人間が効率的な学習が可能になっている可能性がある
・この直感によって教師なしバージョンのカプセルネットワークが新たに開発された
・カプセルネットワークはオブジェクト中心の潜在的特徴表現を学習できる
2.集積カプセルオートエンコーダーとは?
以下、akosiorek.github.ioより「Stacked Capsule Autoencoders」の意訳です。元記事の投稿は2019年6月23日、Adam Kosiorekさんによる投稿です。ヒントン先生が発表したカプセルネットワークの改良版との事で、ヒントン先生ご自身がTwitterで紹介されていた記事です。
オブジェクトは、コンピュータビジョン、そして機械学習研究においてますます中心的な役割を果たしています。画像およびビデオにおけるオブジェクト検出(物体検出)に依存する多くの用途では、正確かつ効率的なアルゴリズムに対する需要が高いです。
より一般的にも、オブジェクトについて知ることは、私たちの環境を理解し対話するために不可欠です。
通常、オブジェクト検出は教師付き学習問題として扱われ、現在の一般的なアプローチは、オブジェクトが与えられた画像の特定の位置に存在するかどうかの確率を予測するCNNをトレーニングする事で行われます。
この方法はオブジェクト検出において超人的な性能を達成することができますが、それらを行うためには膨大な量のデータが必要になります。
これは、ごくわずかな情報からオブジェクトを認識し、位置を特定することを学ぶ子供(または哺乳類)とは非常に対照的です。
何故、哺乳類は非常に効率的に学習できるか?という問いかけに正確に答える事は困難ですが、洗練されたコンピューティングハードウェア(すなわち脳)に存在する、自己教師(self-supervision)と帰納的バイアス(inductive biases)の双方が大きな役割を果たしていると想像できます。
この直感によって、教師なしバージョンのカプセルネットワークが開発されました。概要については以下の図1を参照してください。帰納的バイアスは、オブジェクト中心の潜在的特徴表現を生じさせます。これは、単に入力画像を再構築することによって、自己教師的な方法で学習されます。
学習した特徴表現をクラスタリングすることで、MNIST(98.5%)およびSVHN(55%)で教師なしの最先端の分類性能を達成できるようになりました。
この投稿の残りの部分では、これらの帰納的バイアスとは何か、それらがどのように実装されているのか、そしてこの新しいカプセルアーキテクチャーでどのようなことが可能かを説明します。 また、この新しいバージョンが以前のバージョンのカプセルネットワークとどのように異なるのかについても説明します。
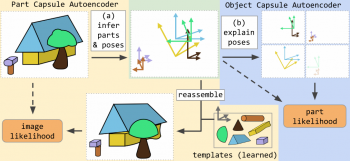
図1
集積カプセルオートエンコーダ(SCAE:Stacked Capsule Autoencoder)は、パーツカプセルオートエンコーダ(PCAE:Part Capsule Autoencoder)とそれに続くオブジェクトカプセルオートエンコーダ(OCAE:Object Capsule Autoencoder)から構成されます。画像をパーツに分解し、そのパーツをオブジェクトとしてグループ化することができます。
なぜ等価性(equivariances)を気にする必要があるのですか?
CNNや2012年のAlexNetの論文がなければ、ディープラーニングがここまで人気が出る事はなかったと言えるでしょう。CNN、畳み込みネットワークは、
(1)局所的な結合性
(2)空間的位置をパラメータで共有
のために、非畳み込み型の画像識別モデルよりも早く学習する事ができます。
前者は学習できるものを制限しますが、近くの画素同士の相関を学習するためには十分で、この相関が画像にとって重要であることがわかります。
後者のパラメータ更新はより多くの信号から恩恵を受ける事が出来るようになるため、学習をより簡単にします。これはまた、変換等価性(translation equivariance)をもたらします。これは、CNNへの入力がシフトされると、出力は等しい量だけシフトされ、それ以外は変化しないままであることを意味します。
形式的には、関数f(x)はT∈T if ∀T∈TTf(x)=f(Tx)
つまり、関数の入力に変換を適用すると、その変換を関数の出力に適用したのと同じ効果があります。
不変性(Invariance)は関連する概念です。
∀T∈Tf(x)=f(Tx)
つまり、入力に変換を適用しても出力が変化しない場合、関数fは不変です。
等価性は、学習時や一般化に役立ちます。例えば、モデルは、分類方法を学習するために、あらゆる空間位置に配置されたオブジェクトを見る必要がなくなります。
これを実現するために回転、拡大、剪断などの各アフィン変換に対応するニューラルネットを用意することは素晴らしいことですが、これを達成するのはそれほど簡単ではありません。(例えばgroup equivariant conv netsを参照)
さまざまな変換に対する等価性はおおよそ学ぶことができますが、それには膨大なデータ拡張が必要です。ランダムに画像を切り抜いたり移動する事で学習用画像データを水増しする事は、変換等価性に対応したCNNをトレーニングする際にも役立ちます。これらの後には通常、fully-connectedレイヤーが続き、それらは異なる位置を処理することを学ぶ必要があるためです。
切り抜きや移動以外のアフィン変換でデータを水増しすることは、簡単ではありません。それは完全な3次元モデルへのアクセスを必要とするためです。モデルが利用可能であったとしても、異なる変換の組み合わせでデータを増やす必要がでてきます。そしてそれは途方もなく巨大な量のデータセットになるでしょう。
オブジェクトがパーツから構成されていることが多く、オブジェクトを構成するパーツは様々な組み合わせを取り得るため、可能な構成を全て取り込むのが最善であるという事実によって、問題は悪化します。Spatial Transformer Networksおよびこのフォローアップ研究は、アフィン変換による等価性を学習する1つの方法を提供しますが、オブジェクトが局所的な変換を受ける事があるという事実には対処できません。
3.集積カプセルオートエンコーダー(1/6)関連リンク
1)akosiorek.github.io
Stacked Capsule Autoencoders
2)openreview.net
Matrix capsules with EM routing
3)arxiv.org
Group Equivariant Convolutional Networks
Spatial Transformer Networks



コメント