Google AIプリンストン研究所で行われる現在および将来の研究(1/2)

１．Google AIプリンストン研究所で行われる現在および将来の研究(1/2)まとめ

・来年、プリンストン大学の側にGoogleが新しく研究所を開設予定
・新しい研究所では大規模機械学習の最適化や制御理論および強化学習が注力される
・大規模機械学習の最適化として新しい手法であるGGTが開発されている

２．AdaGradやAdamに匹敵する性能をもつGGTとは？

以下、ai.googleblog.comより「Google AI Princeton: Current and Future Research」の意訳です。元記事の投稿は2018年12月18日、Elad HazanさんとYoram Singerさんによる投稿です。後半はこちら。

グーグルは長年にわたり学術界と提携して研究を進め、世界中の大学と共同プロジェクトの研究を行ってきました。その結果、コンピュータサイエンス、エンジニアリング、および関連分野で新しい開発が行われています。本日、私たちは、来年初めにプリンストン大学の歴史的なナッソーホール(アメリカ独立戦争時代からあり国会が開催された事もある歴史的建造物)の側に新しい研究所を設立し、新たに学術パートナーシップを提携する事を発表します。

プリンストン大学の教員や学生とより緊密な協力関係を促進することによって、研究所は機械学習の複数の分野で研究を行う事を目指しますが、当初、注力する分野は大規模機械学習の最適化、制御理論および強化学習と予定です。以下に、これまでの研究の進捗状況を簡単に概説します。

大規模機械学習の最適化
あなたが山にハイキングに行き、水がなくなったと想像してください。あなたは湖にたどり着く必要があります。どのようにしてそれを最も効率的に実現できるでしょうか？これはあなたの進むべき方向を最適化する問題と考える事ができます。数学的に言えば勾配降下法と言います。

さて、あなたは坂道の一番最後に湖が見つかる事を期待して、最も急な坂道を下る方向に歩いていきます。湖の位置はその地域で一番低い場所にあるはずなので、数学的に言えば局所的最小値と呼ばれます。喉が渇いているあなたは、できるだけ速く湖にたどり着くために下の図に示すような経路で湖を目指そうとするでしょう。このように勾配を辿る事を勾配降下法と言います。

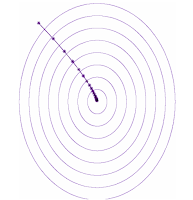
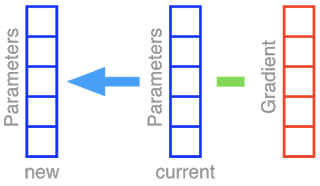
勾配降下法(GD:Gradient Descent)、およびそのランダム化版である確率的勾配降下法(SGD:Stochastic Gradient Descent)は、ニューラルネットワークの重みを最適化するための手法です。ニューラルネットワークの全てのパラメータを箱にまとめたセットを考えましょう。一つ一つの箱は方向を表現しており、数学的に言えばベクトルです。単純に考えるため、このニューラルネットには5つの異なるパラメータしかないと仮定します。勾配降下法を実施する事は、現在のパラメータセット(青い箱)から勾配ベクトル(赤い箱)を減算し、その結果を元のパラメータセットに反映させる事に該当します。

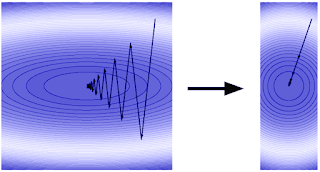
さて、ハイキングの例に戻ると、視界が開けていないため、あなたは地図に載っていない細長い道を左図のようにジグザグに下っていく事になるでしょう。これが勾配降下法です。

しかし、地形を歪める方法があれば、貴方はより早く進むことができます。つまり、地形が左図ではなく右図のようになっていれば貴方はより早く湖まで前進することができます。勾配降下法では、この高速化手法をアクセラレーションと呼びます。一般的な高速化手法は、アダプティブ正則化、またはアダプティブプレコンディショニングと呼ばれ、スタンフォード大学のJohn Duchi教授がGoogleに在職中に共同で考案したAdaGradアルゴリズムによって初めて提案されました。

このアイデアは、勾配降下法を機能しやすくするために湖までの地形を変更することです。そのためには、前処理を行って空間を広げて回転させます。前処理後の地形は、右上図のように完全に円形な湖のように見えます。こうなったら湖までは直線でたどり着けます！具体的には、パラメータベクトル自体から勾配ベクトルを直接差し引く代わりに、以下に示すように、アダプティブプレコンディショニングでは、まずマトリックスプレコンディショナーと呼ばれる5×5の行列で勾配が乗算されます。

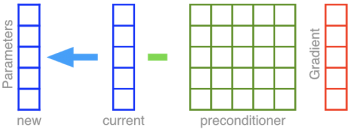
この事前調整操作では、引き伸ばされ、回転された勾配を生成し、それは窪みに向かってはるかに速く進む事を可能にします。ただし、事前調整作業は、その計算量に欠点があります。５次元パラメータベクトルから５次元勾配ベクトルを差し引くのは一回の引き算で完了しますが、前処理変換をするとしたら５×５＝２５の乗算が必要になります。1000万のパラメータを持つディープネットワークを学習するために、勾配を事前調整したいとしたらどうなるでしょう？最小の演算ステップ単位で考えると100兆回相当の演算が必要になります。計算量を節約するために、前処理を回転処理を使わずに引き延ばし処理のみで実現する対角版もオリジナルのAdaGrad論文で紹介されました。対角版は後に修正されて、Adamと呼ばれる別の非常に成功したアルゴリズムを生み出しました。

Adam、つまりこの単純化された対角版の事前調整は、勾配降下法にわずかな追加計算コストのみを課します。しかしながら、過度に単純化することはそれ自身に欠点をもたらします。私たちはもはや自分の空間を回転させることができません。ハイキングの事例に戻ると、狭い峡谷が南東から北西に斜めに走っているならば、私達はもはや西に大きく飛躍することはできません。

私たちが貴方に北東を北極として指し示す用に調整したコンパスを提供したならば、貴方は以前のように西に進んで下降する事ができるでしょう。高次元空間で、コンパスの代理として使用されるのはフルマトリックスプレコンディショニングです。そこで私達は、座標回転機能と同等になるように考慮しながら、計算上効率的な事前調整方法を考案することができるかどうか自問自答しました。

Google AI プリンストンでは、一般的に使用されている対角制限とほぼ同じ計算コストのフルマトリックスアダプティブプレコンディショニングの新しい手法を開発しました。詳細は論文「The Case for Full-Matrix Adaptive Regularization」に記載していますが、この手法の背後にある重要な概念を以下に示します。

完全な行列を使用する代わりに、前処理行列を3つの行列の積で置き換えます。つまり、縦長の行列、小さい四角形の行列、および横長の行列です。膨大な量の計算は、より小さい行列を用いて実行されます。単一の大きなd x d行列の代わりに、GGT(Gradient GradientT)によって計算される行列は、それぞれ、d x k、k x k, k x dとなります。

アルゴリズムの「ウィンドウサイズ(許容できる適切なサイズ)」と考えることができるkを合理的に選択すれば、計算上のボトルネックは単一の大きな行列の積よりはるかに小さなk x k行列まで軽減されます。私達が実際に確かめたところ、典型的には、例えばkを50にし、そしてより小さな正方行列を維持することは、優れた性能をもたらしながら計算量を著しく少なくする事ができます。標準的なディープラーニングタスクに関する他の最適化手法と比較しても、GGTはAdaGradおよびAdamに匹敵する性能です。

(Google AIプリンストン研究所で行われる現在および将来の研究(2/2)に続きます。)

３．Google AIプリンストン研究所で行われる現在および将来の研究(1/2)感想

昨日の量子ニューラルネットワークの記事では超高次元空間では勾配降下法が不毛な台地(barren plateaus)に陥って役に立たなくなると言う話が出ていましたが、本日再び、勾配降下法の詳しい解説が出たのはタイムリーですね。

しかし、大規模機械学習で計算量を減らすためにGGTが開発されていると言う事は、大規模機械学習レベルであれば、勾配降下法はまだ有効であると言う事ですよね。そうすると、量子ニューラルネットワークが相手をする超高次元空間とはいったいどんなレベルのものであるのか、少し頭がクラクラしてきますが、「これが超高次元空間だ！」と二次元を見ながら叫んで対処するしかないのですかね。