線形回帰とロジスティック回帰の違い

１．線形回帰とロジスティック回帰の違いまとめ

・線形回帰とロジスティック回帰は使う場面が全く違うが名前が紛らわしく混乱を招く
・線形回帰はその名の通り線であり数値で表現できる何かを予測する際に使う
・ロジスティック回帰は数値で表現する事が出来ない何かを分類する際に使う

２．Linear RegressionとLogistic Regression

以下、www.kdnuggets.comより「Linear vs Logistic Regression: A Succinct Explanation」の意訳です。元記事は2022年3月、Nisha Aryaさんによる投稿です。

線形回帰とロジスティック回帰は使う場面が全く違いますが、確かに名前が紛らわしく混乱を招くためか、元サイトでもアクセス数の多い人気記事となっていました。

試験対策などで簡単に覚えるのでしたら、線形回帰はその名の通り線でありy=ax+b形式の数値で表現できる何かを予測する際に使う。ロジスティック回帰はその名の通り論理であり「女性と男性」のように数値で表現する事が出来ない何かを分類する際に使う、の理解で良いのかな、と思います。

アイキャッチ画像はlatent diffusionでプロンプトはLinear Regression vs Logistic Regression

線形回帰とロジスティック回帰は、どちらも教師あり学習から分岐した2つのよく使われる機械学習アルゴリズムです。線形回帰は回帰の問題を解決するために使用され、ロジスティック回帰は分類の問題を解決するために使用されます。詳しくは以下をご覧ください。

線形回帰(Linear Regression)とロジスティック回帰(Logistic Regression)はどちらも「L」で始まり、「Regression」で終わるので、混同するのも無理はありません。Linear RegressionとLogistic Regressionはよく使われる機械学習アルゴリズムで、どちらも教師あり学習から分岐しています。

簡単に説明します。

教師あり学習は、アルゴリズムがラベル付けされたデータセットを使って学習し、学習データを分析することです。これらのラベル付きデータセットには入力と期待される出力があります。

教師なし学習はラベルの付いていないデータで学習し、隠れた構造を推測して正確で信頼できる出力を生成します。

線形回帰とロジスティック回帰の関係は、ラベル付けされたデータセットを使って予測を行うということです。しかし、両者の主な違いは、それらがどのように使用されているかということです。線形回帰は回帰(Regression)の問題を解決するために使われ、ロジスティック回帰は分類(Classification)の問題を解決するために使われます。

分類は、異なるパラメータに基づいて分類対象がどのカテゴリに属するかを識別し、ラベルを予測することです。

回帰は、従属変数と独立変数の間の相関を見つけることによって、連続的な出力を予測することです。

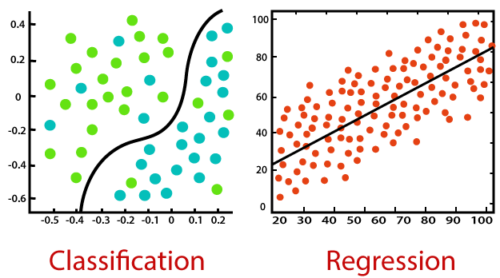
線形回帰

線形回帰は、教師あり学習から分岐した最も単純な機械学習アルゴリズムの1つとして知られており、主に回帰問題を解決するために使用されます。

線形回帰の用途は、独立変数から支援と知識を得て、連続的な従属変数の予測を行うことです。線形回帰の全体的な目標は、連続的な従属変数の出力を正確に予測できる最適な直線を見つけることです。連続値の例としては、住宅価格、年齢、給与などがあります。

単回帰(Simple Linear Regression)は、1つの独立変数と1つの従属変数の関係を直線を用いて推定する回帰モデルです。独立変数が2つ以上ある場合は、重回帰(Multiple Linear Regression)と呼びます。

最良適合線という戦略を用いることで、従属変数と独立変数の間の関係を理解するのに役立ちます。それは線形であるべきです。

線形回帰の公式

高校の数学を覚えている人なら、y = mx + b という公式を覚えているでしょう。これは、直線の傾きと切片を表しています。

‘y’ と ‘x’ は変数、’m’ は直線の傾き、’b’ は直線がy-軸を交差するy-切片(y-intercept)を表します。

線形回帰では、「y」は従属変数、「x」は独立変数、「B0」はy切片、「B1」は独立変数と従属変数の間の関係を表す傾きを表します。

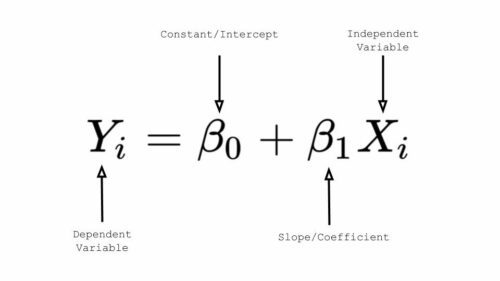
ロジスティック回帰

ロジスティック回帰は、教師あり学習から分岐した機械学習アルゴリズムの1つで、非常に人気があります。ロジスティック回帰は、回帰と分類の両方のタスクに使用できますが、主に分類に使用されます。

0か1、yesかno、またはtrueとfalseを使用して、今日雨が降るかどうかを予測する事などがロジスティック回帰の例です。

ロジスティック回帰の使用は、独立変数の支援と知識を得て、カテゴリ従属変数を予測することです。ロジスティック回帰の全体的な目的は0 と 1 の間にしかない出力を分類することです。

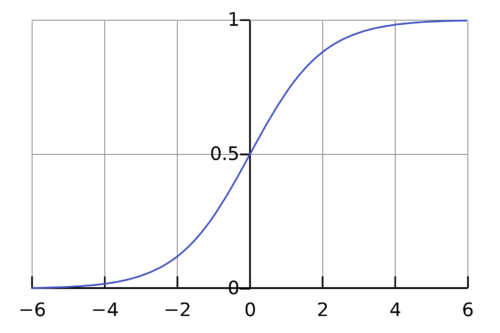
シグモイド関数の公式

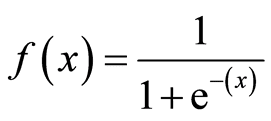
線形回帰とロジスティック回帰

ロジスティック回帰は、最尤推定(Maximum Likelihood Estimation)に基づいています。これは、いくつかの観察されたデータから、仮定された確率分布のパラメータを推定する手法です。

コスト関数(Cost Function)

コスト関数とは、誤差を計算するための数式で、予測値と実際の値の差です。これは、xとyの関係を推定する能力という点で、モデルがどの程度間違っているかを単純に測定するものです。

線形回帰のコスト関数

線形回帰のコスト関数は、2乗根平均誤差(root mean squared error)、または平均2乗誤差(MSE:mean squared error)としても知られています。

MSEは、観測された実際の値と予測値の間の平均2乗差を測定します。コストは、現在の重みのセットと関連する1つの数値として出力されます。コスト関数を使用する理由は、モデルの精度を向上させるためで、MSEを最小化することでこれを実現します。

MSEの計算式は以下の通りです。

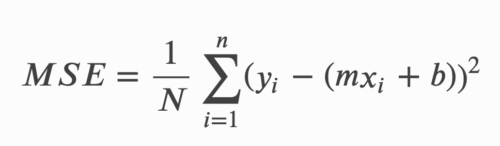
ロジスティック回帰のコスト関数

ロジスティック回帰のコスト関数は、予測関数が非線形(シグモイド変換が行われるため)なので、MSEを使うことができません。したがって、クロス・エントロピー(Cross-Entropy。Log Lossとも呼ばれます)と呼ばれるコスト関数を使用します。

クロス・エントロピーは、与えられた確率変数またはイベントの集合に対する2つの確率分布の間の差を測定します。

クロス・エントロピーの計算式

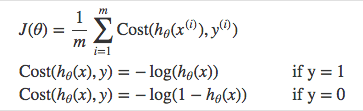
線形回帰とロジスティック回帰の比較

線形回帰(Linear Regression)	ロジスティック回帰(Logistic Regression)
任意の独立変数の集合を使用して、連続従属変数を予測するために使用する	独立変数のセットを使用して、カテゴリ従属変数を予測するために使用する
生成される出力は、価格や年齢などの連続値でなければならない	生成される出力は、0 または 1、Yes または No のようなカテゴリ値でなければならない
従属変数と独立変数の間の関係は線形でなければならない	従属変数と独立変数の間の関係は、線形である必要はない
回帰問題を解くために使用される	分類の問題を解くために使用される
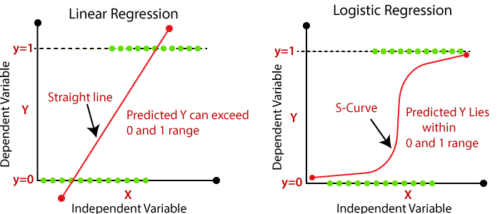
出力を簡単に予測するために、最適な直線を見つけて使用する	S字カーブ(シグモイド)を使って、予測された出力を分類する
精度の推定には最小二乗法が使用される	精度の推定には最尤推定法を用いている
独立変数間に共線性がある可能性がある	独立変数間に共線性があってはならない