DeepCTRL:ニューラルネットワークにルールを教えて制御する試み(2/3)

１．DeepCTRL:ニューラルネットワークにルールを教えて制御する試み(2/3)まとめ

・ルールベースの目標を用いた学習ではパラメータに対して目標が微分可能な事が必要
・入力特徴量に小さなランダムノイズを加える事で非微分的制約に対応可能な手法を開発
・DeepCTRLはより高い精度を達成しつつ、かつルールに適切に従う事が可能

２．DeepCTRLの性能

入力に小さなノイズを加える事でルールを統合

ルールベースの目標を用いた学習では、モデルの学習可能なパラメータに対して目標が微分可能であることが必要です。

しかし、入力に対して微分不可能な価値あるルールも多く存在します。例えば、「血圧が140より高いと心血管疾患になりやすい」というルールは、従来のDNNに組み込む事が難しいルールです。

そのため、入力特徴量に小さな摂動(ランダムなノイズ)を導入し、結果が望ましい方向にあるかどうかでルールベースの制約を構成することで、DeepCTRLを非微分的制約に一般化する新しい入力摂動手法(novel input perturbation method)を紹介します。

使用例

ルールの活用が特に重要な物理学や医療分野での機械学習事例でDeepCTRLを評価します。

・物理学における既知の原理を考慮した信頼性の向上
モデルの信頼性を検証率(verification ratio、ルールを満たす出力サンプルの割合)で定量的に評価します。特に自然科学のようにルールが常に有効であることが分かっている場合、より良い検証率で運用することが有益となります。制御パラメータαを調整することで、より高いルール検証率、ひいてはより信頼性の高い予測を達成することができます。

このことを示すために、二重振り子の動きから生成される時系列データを考えます。二重振り子は、与えられた初期状態から摩擦を伴って動く事とし、課題は、エネルギー保存則を適用しながら、現在の状態から二重振り子の次の状態を予測することと定義します。

この規則をどの程度学習したかを定量的に評価するために、以下で検証率を評価します。

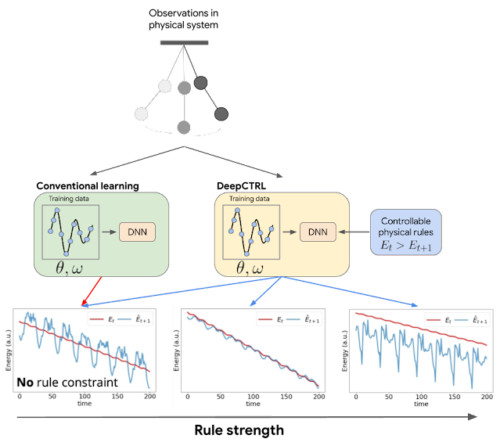
DeepCTRLは、学習完了後に再学習せずともモデルの挙動を制御することが可能です。二重振り子の例では、従来手法の学習では、モデルが物理法則(例えば、エネルギー保存則)に従うことを保証するための制約を課す事ができません。ルール強度が低いDeepCTRLの場合も、状況は同様です。そのため、時刻t+1において予測されるシステムの総エネルギー(青)は、時刻tにおいて測定されたエネルギー(赤)よりも大きくなることがあり、これは物理法則に違反するので許容されません(左下図)。DeepCTRLのルール強度が高い場合、モデルは与えられたルールに従いますが精度が落ちることがあります。(右下図：赤と青の間の不一致が大きくなる)ルール強度が両極端の間にある場合、モデルはより高い精度を達成し(青の曲線は赤に近い)、かつルールに適切に従う(青の曲線は赤の曲線より低い)可能性があります。

この課題に対するDeepCTRLの性能を、従来手法と比較します。従来手法では目的に正則化項(regularization term)として固定ルールベースの制約を加えて学習を行います。この正則化係数が最も高い場合、検証率は最も高くなりますが(下記二番目のグラフ緑線)、予測誤差はλ=0.1(オレンジ線)に比べて若干悪くなっています。

ルールを固定した従来手法の予測誤差の最小値はDeepCTRLと同等ですが、検証率の最大値はやはりルール固定手法の方が低く、DeepCTRLがエネルギー保存則に従いながら正確な予測を行えることを示唆していることが分かります。

さらに、ラグランジュ・デュアル・フレームワーク(LDF:Lagrangian Dual Framework)を用いてルール制約を課すベンチマークを検討し、そのハイパーパラメータを、検証セット上で最も低い平均絶対誤差(LDF-MAE)と最も高いルール検証比(LDF-Ratio)を選んで図示した2つの結果を以下に示しました。LDF法の性能は、主制約が何であるかに非常に敏感であり、その出力は信頼性がありません(黒とピンクの破線)。

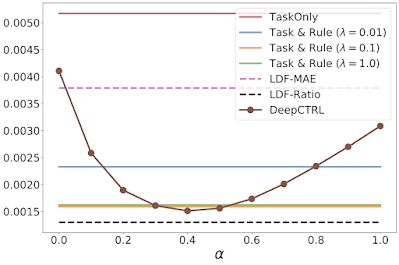
二重振り子タスクの実験結果：タスクベースの平均絶対誤差(MAE:mean absolute error)
つまり本当の計測値とモデル予測の間の不一致を測定し、制御パラメータαをX軸にしてDeepCTRLと比較しました。TaskOnlyはルール制約がなく、Task & Ruleには異なるルール強度(λ)が設定されています。LDFは制約最適化問題を解くことでルールを強制します。

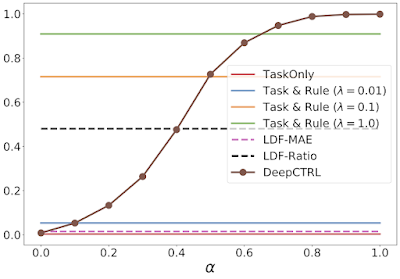
上記と同条件ですが、検証率を示しています。

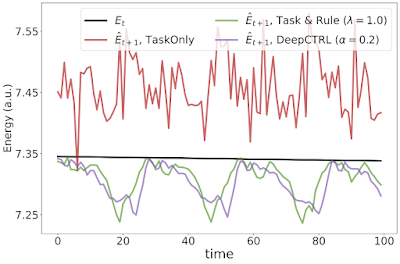
二重振り子タスクの実験結果
時刻tとt+1における現在のエネルギーと予測されるエネルギーをそれぞれ示しています。