Neural Tangents：高速に手軽にニューラルネットワークの幅を無限に拡張(1/2)

１．Neural Tangents：高速に手軽にニューラルネットワークの幅を無限に拡張(1/2)まとめ

・最近の多くの研究結果はDNNの幅を無限に拡張していくとガウス過程に収束していく事を示している
・この収束が有効である限り勾配降下の収束などの複雑な現象も単純な線形代数方程式に要約される
・しかし無限幅ネットワークを導き出すには非常に困難だがそれを簡単に実現できるのがNeural Tangents

２．Neural Tangentsとは？

以下、ai.googleblog.comより「Fast and Easy Infinitely Wide Networks with Neural Tangents」の意訳です。元記事の投稿は2020年3月13日、Samuel S. SchoenholzさんとRoman Novakさんによる投稿です。

アイキャッチ画像はガウスつながりでガウシアンぼかしがかかっている花の写真でクレジットはPhoto by Aaron Burden on Unsplash

自然言語処理、会話エージェント、コネトミクスなどのさまざまな領域にわたるディープラーニングの広範囲な成功により、機械学習の研究の展望が変わり、研究者に次のような興味深い重要な未解決の質問が残されました。

・ディープニューラルネットワーク(DNN)は過度にパラメーター化されているにもかかわらず、なぜこれほどうまく一般化出来るのですか？
・ディープネットワークのアーキテクチャ、トレーニング、パフォーマンスはどのような関係にありますか？
・ディープラーニングモデルから顕著な特徴表現をどのように抽出できますか？

近年の進歩を可能にした重要な理論的洞察の1つは、DNNの幅を広くすると、より規則的な動作が得られ、理解しやすくなるということです。最近の多くの研究結果は、DNNの幅を無限に拡張していくと、ガウス過程(Gaussian process)と呼ばれる別のより単純なクラスのモデルに収束していく事を示しています。

この収束が有効である限り、複雑な現象(ベイジアン推論や畳み込みニューラルネットワークの勾配降下の収束過程の変遷など)は、単純な線形代数方程式に要約されます。これらの無限に広いネットワークからの洞察は、しばしばそれらの有限の対応するものに引き継がれます。そのため、無限幅のネットワークは、ディープラーニングを研究するためのレンズとして使用できますが、それ自体が有用なモデルとしても使用できます。

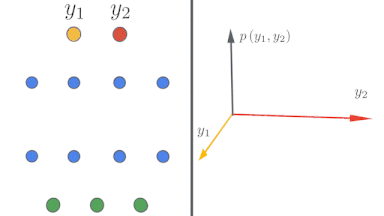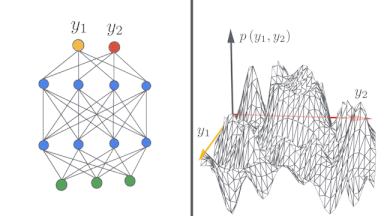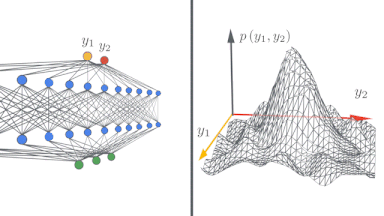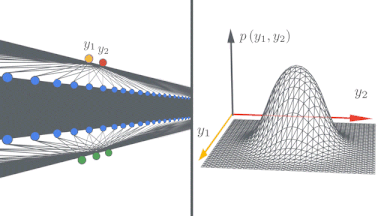
左：ディープニューラルネットワークが単純な入力/出力マップを無限に広くするにつれてどのように変化するかの概略図
右：ニューラルネットワークの幅が大きくなると、ネットワーク出力がガウス分布に近づく事がわかります。

残念ながら、有限幅ネットワークから無限幅ネットワークを導き出すには、かなりの数学的専門知識が必要であり、研究対象のアーキテクチャごとに個別に解決する必要があります。

更に無限幅モデルが導出された後、効率的でスケーラブルな実装を考え出すには、かなりのエンジニアリング能力が必要になります。

合わせて、有限幅モデルを対応する無限幅ネットワークに取り込むプロセスは数か月かかる可能性があり、それ自体が研究論文のトピックになるほど大変な可能性があります。

この問題に対処し、ディープラーニングの理論的進歩を加速するために、私達はNeural Tangentsを発表します。

Neural TangentsはJAXで書かれた新しいオープンソースソフトウェアライブラリで、これを使うと、研究者は有限ニューラルネットワークと同じくらい簡単に無限に広いニューラルネットワークを構築およびトレーニングできます。Neural Tangentsの核となるのは、ニューラルネットワークの有限幅バージョンと無限幅バージョンを同時に構築する使いやすいニューラルネットワークライブラリです。