1.Minerva:大学受験レベルの数学を解答可能な言語モデル(1/2)まとめ
・定量的推論は、言語モデルがまだ人間レベルの性能にはるかに及ばない分野の一つ
・数学問題を解くには数学的表記や数式や定数の記憶、段階的な推論などが必要なため
・Minervaは電卓などの外部ツールに頼ることなく数学問題を解答可能な大規模言語モデル
2.Minervaとは?
以下、ai.googleblog.comより「Minerva: Solving Quantitative Reasoning Problems with Language Models」の意訳です。元記事は2022年6月30日、Ethan DyerさんとGuy Gur-Ariさんによる投稿です。
数式を含む自然言語で学習させたため、科学技術問題を解答可能な人工知能Minervaですが、まだ誤答するケースもあるそうです。しかし、人工知能が誤答すると「真の意味で理解をしていない」となりがちですが、人間の脳はミスをするのに、人工知能はミスを許されないのは暗黙のうちに「脳の柔軟性」と「機械の完璧性」の両立を求められているからのような気も最近してきました。人間レベルのAI(HLAI:Human Level AI)って実は超人間レベルですね。
アイキャッチ画像はメキシコのミネルバ像でクレジットはPhoto by Roman Lopez on Unsplash
言語モデルは、様々な自然言語タスクで顕著な性能を発揮してきました。実際、BERT、GPT-3、Gopher、PaLMなど多くの研究から得られる汎用的な教訓は、大規模で多様なデータを使って教師なし方式で学習したニューラルネットワークは、様々なタスクで優れた性能を発揮できるということでした。
定量的推論(Quantitative reasoning)は、言語モデルがまだ人間レベルの性能にはるかに及ばない分野の一つです。数学的・科学的な問題を解くには、自然言語と数学的表記法を用いて問題を正しく解析すること、関連する数式や定数を思い出すこと、数値計算や記号操作を含むステップバイステップの解を生成することなど、さまざまなスキルを組み合わせる必要があります。このような課題から、機械学習を用いた定量的推論問題の解決には、モデルのアーキテクチャや学習技術の大幅な進歩、Pythonインタープリタなどの外部ツールへのアクセス権の付与、あるいは、より深刻なパラダイムシフトが必要だと考えられています。
論文「Solving Quantitative Reasoning Problems With Language Models」(近日中にarXivにて公開予定)では、数学や科学の問題を段階的推論(step-by-step reasoning)で解決する言語モデル、Minervaを紹介します。
定量的推論問題に関連する学習データの収集に注力し、モデルを大規模に学習させ、クラス最高の推論技術を採用することで、様々な困難な定量的推論タスクにおいて大幅な性能向上を達成することを示します。Minervaは、電卓などの外部ツールに頼ることなく、数値計算や記号操作を含む解答を生成することで、このような問題を解決します。
このモデルは、自然言語と数学的表記法を組み合わせて、数学的な質問を解析し、回答します。Minervaは、小数回プロンプト、思考の連鎖(chain of thought)やスクラッチパッドのプロンプト、多数決などの技術を組み合わせて、STEM推論タスクにおいて最先端の性能を達成します。Minervaの出力は、インタラクティブなサンプルエクスプローラーで調べることができます。

多段階の問題を解く:MATHデータセットの問題とMinervaの解答
このモデルは、一次方程式を書き下ろし、それを単純化し、変数を代入し、yについて解きます。
多段階定量的推論のために構築されたモデル
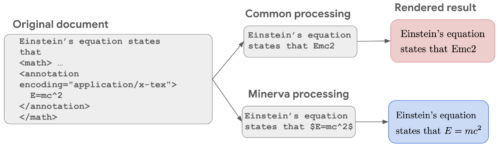
Minervaは、Pathways Language Model(PaLM)をベースに、arXivのプレプリントサーバーにある118GBの科学論文データセットと、LaTeXやMathJaxなどの数式を含むWebページでさらに学習させることで、定量的推論を促進させています。
標準的なテキストクリーニングプロセスでは、数学式の意味上不可欠な記号や書式が削除されることがよくあります。このような情報を学習データとして保持することで、モデルは標準的な数学表記を用いた会話を学習することができます。

工学部などを志望するインドの高校生約200万人が毎年受験する「合同入学試験本科数学2020」(左)と、毎年約27万人の高校生が受験するポーランドの「全国数学検定試験2022年5月」の問題例(右)
定量的な推論を行うためのデータセット。丁寧なデータ処理により数学的情報を保持し、より高度な数学の学習を可能にします。
Minervaはまた、数学的な問題をよりよく解くために、最近のプロンプトと評価のテクニックを取り入れています。例えば、思考の連鎖(chain of thought)やスクラッチパッドプロンプティング(scratchpad prompting:Minervaに新しい問題を提示する前に、既存の問題に対するいくつかのステップバイステップの解答を提示する)、多数決(majority voting)などがあります。
多くの言語モデルと同様に、Minervaは様々な可能性のある出力に確率を割り当てます。質問に答えるとき、Minervaが最も可能性が高いと判断した1つの解答を選ぶのではなく、可能性のあるすべての出力から確率的にサンプリングして複数の解答を生成する。これらの解答は異なりますが(例えば推論ステップが同一でないなど)、しばしば同じ最終解答に到達します。Minervaはこれらのサンプリングされた解答に対して多数決を行い、最も共通する結果を決定的な最終解答として採用します。

多数決方式:Minervaは各質問に対して複数の解答を生成し、最も共通する解答を選択することで、パフォーマンスを大幅に改善します。
3.Minerva:大学受験レベルの数学を解答可能な言語モデル(1/2)関連リンク
1)ai.googleblog.com
Minerva: Solving Quantitative Reasoning Problems with Language Models
2)arxiv.org
Solving Quantitative Reasoning Problems with Language Models
3)minerva-demo.github.io
Minerva Explorer



