1.GPT-3の約2倍の性能で算数の文章問題を解く人工知能まとめ
・小学校の算数の問題を微調整したGPT-3モデルの約2倍の精度で解くシステムを開発
・このシステムは、実際の子供たちが出した正答率の約90%の正答率で問題を解くことが可能
・モデルが自分のミスを認識できるように訓練し何度も試行錯誤できるようにして実現
2.検証により正答率を向上
以下、openai.comより「Solving Math Word Problems」の意訳です。元記事の投稿は2021年10月29日、Karl Cobbeさん、Vineet Kosarajuさん、John Schulmanさんによる投稿です。
アイキャッチ画像のクレジットはPhoto by CDC on Unsplash
小学校の算数の問題を、微調整したGPT-3モデルの約2倍の精度で解くシステムを開発しました。このシステムは、実際の子供たちの約90%の問題を解くことができます。9~12歳の子供たちの小集団は、データセットのテストで60%のスコアを出したのに対し、私達のシステムは同じ問題で55%のスコアを達成しました。
現在のAIは、小学生でも簡単にできる常識的な多段階推論がまだ苦手なので、この点は重要です。このような結果が得られたのは、モデルが自分のミスを認識できるように訓練することで、うまくいく解決策が見つかるまで何度も試行錯誤できるようになったからです。
はじめに
GPT-3のような大型言語モデルは、多様な文体を模倣する能力や、豊富な事実認識能力など、多くの優れた能力を持っています。しかし、このような大型な言語モデルであっても、小学校の算数の文章問題を解くような、多段階の正確な推論を必要とするタスクをこなすのに苦労します。GPT-3は、正しい解答の流れを真似ることはできますが、致命的な論理ミスを頻発します。
複雑な論理的領域で人間と同等のパフォーマンスを発揮するためには、モデルが自分のミスを認識し、慎重にステップを選択することを学ばなければなりません。そのために、提案された解決策が正しいかどうかを評価する検証者(verifiers)を育成します。新しい問題を解決するために、検証者は多くの提案された解決策の中から最適なものを選択します。我々の手法を評価するために、新しいGSM8Kデータセットを収集し、研究を促進するためにこのデータセットを公開しています。
以下の例では,我々の新しい手法である検証(verification)と、比較対象手法である微調整(fine-tuning)によって生成された解を示しています。
Aliのクラスの定員は120名です。
Johnの各クラスの定員は、120/8=15人です。
Johnの2クラスの定員の合計は、15人×2クラス=30人です。
2つの学校の合計定員は、120人+30人=150人です。
Johnの各クラスの定員は、120人÷8=15人です。
つまり、Johnが担当する2つのクラスの定員は、合計で15人×2=30人です。
Aliのクラスの定員は、120人×1=120人です。
したがって、Aliの学校の合計収容人数は、120人+30人=150人となります。
したがって、両校の合計収容人数は150人+30人=180人です。
各クラスの定員がAliのクラスの1/8とすると、Johnのクラスの定員を合わせると1/8*120=15.0
2つの学校を合わせると、15.0+120=135.0の定員になります。
Aliは1つのクラスに120人の生徒がいて、それぞれのクラスに8人の生徒がいるので、彼は120/8 = 15クラスを持っています。
彼のすべてのクラスの合計容量は15 * 120=1800人です。
Johnは、Aliのクラスの1/8の定員のクラスを2つ持っているので、それぞれのクラスに2*15 = 30人の生徒がいます。
Johnの両クラスの合計収容人数は、30*2=60人となります。
両方の学校の合計収容人数は、1800+60=1860人となります。
GSM8K Dataset
GSM8K(Grade School Math 8K)は、8,500の高品質な小学校の算数の文章問題で構成されています。それぞれの問題は、2から8のステップで解かれ、解答は主に、基本的な算術演算(+ – × ÷)を用いた一連の初歩的な計算を行って最終的な答えにたどり着きます。
このデータセットでは、問題の多様性が高いことが主な原因で、最先端の言語モデルを微調整しても十分な結果が得られません。一方で,GSM8Kの解答は初歩的な概念にしか依存していないため、高いテスト性能を達成することは容易な目標です。
GSM8Kの解法は、純粋な数学的表現ではなく、自然言語で書かれています。自然言語にこだわることで、モデルが生成した解法は人間がより容易に解釈できるようになり、私達の手法は比較的、分野にとらわれないものとなっています。
検証者の育成。誤りから学ぶモデル
数学的推論の大きな課題の一つは、個別のミスに敏感であることです。自己回帰モデルは、各解をトークンごとに生成するため、自分のミスを修正するメカニズムがありません。軌道を外れた解はすぐに回復できなくなります。
この問題を解決するために、モデルが生成した解の正しさを評価する検証者を育成します。検証者には、モデル自身が書いた多くの解答が与えられ、正しい解答があるとすればどれかを判断できるように訓練されます。
テスト時に新しい問題を解くために、100個の解答候補を生成し、その中から検証者が最も高く評価した解答を選びます。検証は、このような固有の選択肢があることに加え、検証は生成よりも単純な作業であることが多いという利点があります。
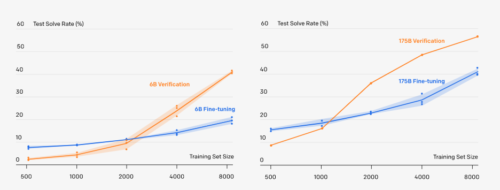
データセットが十分な大きさであれば、検証によって性能が大幅に向上することがわかりました。データセットが小さすぎると,検証者は数学的推論のより有用な特性を学ぶのではなく、訓練セットの最終的な答えを記憶することで過剰適合してしまうと考えられます。
全学習セットにおいて,60億パラメータの検証は、微調整された1750億パラメータモデルをわずかに上回り、モデルサイズを30倍に拡大したのとほぼ同等の性能向上が得られました。更に、現在の結果から推定すると、検証はデータを追加することでより効果的に規模拡大できるようです。
結論
正しい議論を行い、間違った議論を認識することは、より汎用的なAIを開発するための重要な課題です。小学校の算数は、これらの能力の理想的な試験環境です。GSM8Kの問題は概念的には簡単ですが、1つの微妙なミスが全体的な解法を脱線させるのに十分です。そのようなミスを見つけ、回避することは、モデルが開発する上で重要なスキルです。検証者を養成することで、モデルに良い解法とうまくいかなかった解法を分けることを教えます。これらのスキルは、モデルをより論理的に複雑な領域に適用しようとする際に、ますます重要になると考えています。
3.GPT-3の約2倍の性能で算数の文章問題を解く人工知能関連リンク
1)openai.com
Solving Math Word Problems
2)arxiv.org
Training Verifiers to Solve Math Word Problems
3)github.com
openai / grade-school-math




Aliは私立学校の学部長で、1つのクラスを担当しています。Johnも公立学校の学部長です。Johnは自分の学校に2つのクラスを持っています。それぞれのクラスの定員は、Aliのクラスの定員120人の1/8です。両方の学校の合計定員は何人でしょうか?