1.SLaQ:大規模データの形状を理解する(1/2)まとめ
・グラフとは個々の項目が相互にどのように関連しているかを表現する数学モデル
・物体間の関係をモデル化するために広く使用可能でWeb、友人関係、分子構造まで表現できる
・昨年発表したDDGKはグラフの特徴表現を教師なしで学習できるが規模拡大が難しかった
2.SLaQとは?
以下、ai.googleblog.comより「Understanding the Shape of Large-Scale Data」の意訳です。元記事の投稿は2020年5月5日、Anton TsitsulinさんとBryan Perozziさんによる投稿です。
グラフのお話なのですが、グラフと聞いて棒グラフや折れ線グラフをイメージしてしまうと理解が難しくなります。もっと広い概念で「表現しにくいデータをどうにかしてスッキリ表現するための手段」とイメージすると良いと思います。
アイキャッチ画像は一番綺麗なグラフに見えた葉脈の画像でクレジットはPhoto by Vivaan Trivedii on Unsplash
複雑なデータ同士を比較して違いや類似点を理解することは、データを取り扱う際にしばしば発生する興味深い課題です。この課題を定型化する1つの手法は、各データセットをグラフとして表示することです。
グラフは、個々の項目が相互にどのように関連しているかを表現する数学モデルです。物体間の関係をモデル化するために広く使用されています。
インターネットグラフは相互に参照しているWebページの接続状態を表現し、ソーシャルグラフは友人関係をリンクし、分子グラフは相互に結合している原子を表します。
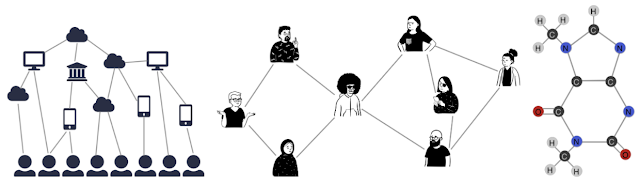
グラフは、Webページ(左)、社会的な関係(中央)、分子構造(右)など、様々なタイプの関係をモデル化できます。
複数のグラフが存在する時、各グラフの属性をまとめて予測したくなる事がよくあります。(例えば、グラフ毎にラベルを一つ付与するなど)
ここで、構造からタンパク質の性質を予測するタスクを考えてみます。ここでの各データセットは1つのタンパク質であり、予測タスクは最終的に構造が酵素を含んでいるかどうかです。モデルを使って実際に予測をする必要があるため、様々なタンパク質の構造全体を一般化できる特徴表現が必要です。
理想的には、コストのかかるラベル付けを行わずにグラフをベクトルとして表す方法が必要です。問題は、グラフのサイズが大きくなるにつれて困難になる事です。分子の場合であれば、人間はその特性についてある程度の知識を持っていますが、より大きく複雑なデータセットを推論することはデータが大きくなるにつれて難しくなります。
本投稿は、WWW’20で発表される論文「Just SLaQ When You Approximate: Accurate Spectral Distances for Web-Scale Graphs」からグラフの特徴表現学習における最近の進歩に焦点を当てます。
これは、WWW’19で公開された以前の研究「DDGK: Learning Graph Representations for Deep Divergence Graph Kernels」を規模を拡大するように改良したものです。
SLaQは、大きなグラフを迅速かつ効率的に特徴付けることができます。特定のグラフ統計を近似するように計算をスケーリングする事でこれを行います。また、Google ResearchのGitHubページにグラフembeddingsに関する論文とコードを公開した事もお知らせします。
グラフの類似性を完全教師なし学習で習得
2019年の論文では、特定分野の知識や教師なしでグラフの類似性の特徴表現を学習できることを示しました。私達が提案したDDGK(Deep Divergence Graph Kernels)は、グラフ上の特徴表現を学習し、グラフ間の類似性を符号化する教師なし学習手法です。
従来の手法とは異なり、私達の教師なし手法は、ノードの特徴表現、グラフの特徴表現、およびグラフ同士をAttentionベースで整列させる事を共同で学習します。
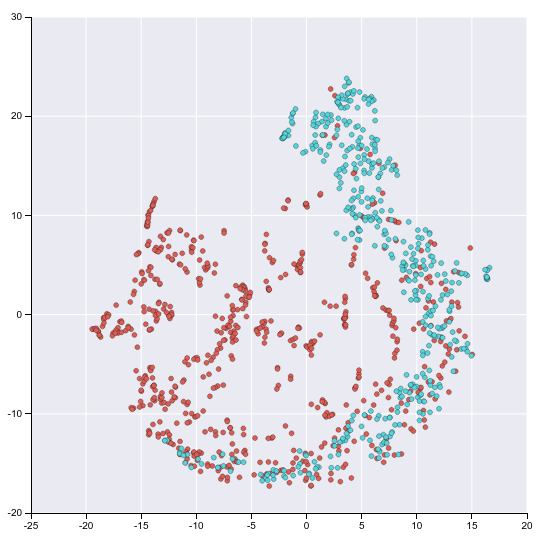
上図は、タンパク質を比較するためにDDGKによって学習された潜在的な特徴表現をt-SNEで視覚化したものです。青い点は酵素を含むタンパク質を示し、赤い点は酵素を含まないタンパク質を示します。
DDGKによる符号化は、酵素を含むか否かに関わらず、タンパク質の構造特性と相関している事がわかります。(本グラフは特徴表現の投影であるため、軸の数値には意味がないことに注意してください)
上記の例は、DDGKがどのようにしてグラフの特徴表現を自動的に学習、及び整列し、潜在的で機能的な類似性を符号化するかを示しています
以下の、他のデータセットを使った実験でも、様々な全く違うタイプのグラフ(言語、生物学、社会的関係)間でも類似点と相違点を捉える事が示されています。
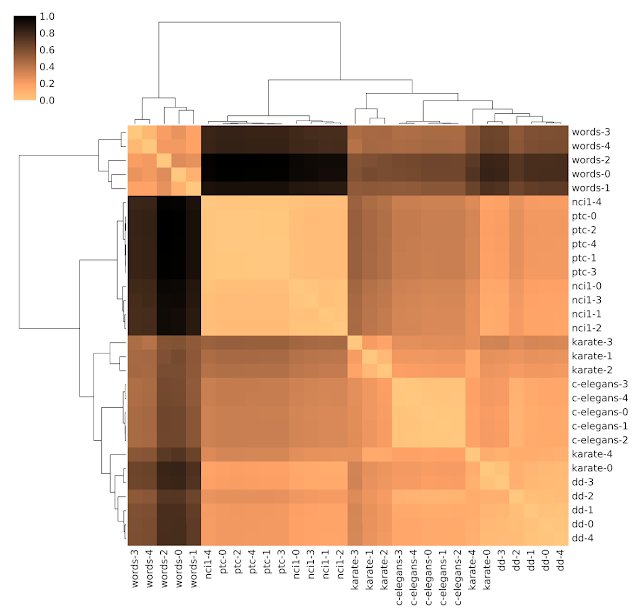
DDGKを使用して符号化および整列された異なるデータセット間のペアワイズ距離
色は潜在空間での距離を示し、類似度は0(同一)から1.0(非常に異なる)の範囲です。特徴表現をクラスター化して類似のデータセットをグループ化できることがわかります。例えば、データセットnci1とptcはどちらも化学物質のデータセットです。
3.SLaQ:大規模データの形状を理解する(1/2)関連リンク
1)ai.googleblog.com
Understanding the Shape of Large-Scale Data
2)github.com
google-research/graph_embedding
3)dl.acm.org
DDGK: Learning Graph Representations for Deep Divergence Graph Kernels
Just SLaQ When You Approximate: Accurate Spectral Distances for Web-Scale Graphs



コメント