FriendlyCore:集約時の誤差を低減する新規差分プライベートフレームワーク(1/2)

１．FriendlyCore:集約時の誤差を低減する新規差分プライベートフレームワーク(1/2)まとめ

・差分プライバシー(DP:Differential Privacy)は個人を特定できないようにしながら全体としての傾向を学習させる機械学習アルゴリズム
・数学的にプライバシー保護を保障するために「ありえないポイント」も考慮してノイズを追加しなければならないので精度が落ちる
・FriendlyCoreはデータが互いに近い「Friendly」な部分(core)を抽出する前処理を行う事でノイズを減らして精度を向上する新手法

２．FriendlyCoreとは？

以下、ai.googleblog.comより「FriendlyCore: A novel differentially private aggregation framework」の意訳です。元記事の投稿は2023年2月15日、Haim KaplanさんとYishay Mansourさんによる投稿です。

差分プライバシーはざっくりいうと、皆さんのPC／スマホからデータ収集してかな漢字変換の予測精度をあげたりする際に使われている技術です。個人を特定できないように収集したデータにノイズを加えつつ、それを使って機械学習を行って予測精度を上げようというお話なので、本質的に矛盾しているのですが、個人情報保護の観点から重視されている技術でもあり、試験問題などにも良く取り上げられ事が多いようです。

アイキャッチ画像はstable diffusionのカスタムモデルによる生成でプロンプトにFriendlyを含めるとやっぱり距離が近くなるんだな、と思いつつ、これだけみたら単なるスナップ写真にも見えてしまう画像

差分プライバシー(DP:Differential Privacy)機械学習アルゴリズムは、各データポイントが集計された出力に与える影響を制限する事を数学的に保証して、ユーザーデータを保護します。直感的には、この保証は、1人のユーザーの貢献度を変更しても、DPアルゴリズムの出力分布が大きく変化することはないことを意味します。

しかし、DPアルゴリズムは、非プライベートなものに比べて精度が落ちる傾向があります。なぜなら、DPを数学的に保障する事は非常に厳しい要件であり、集計に大きな影響を与える「ありえないポイント」を含む、あらゆる潜在的な入力ポイントの変化を「隠す」ためにノイズを追加しなければならないからです。

例えば、あるデータセットの平均をプライバシーを保持したまま推定したいとします。そして、直径Λの球がとり得る全てのデータポイントを含んでいることがわかっているとします。

１つのポイントが平均に与える影響はΛによって制限されるので、DPを確保するためには各座標にΛに比例するノイズを加えれば十分です。

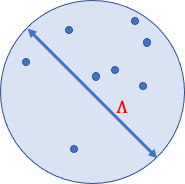
すべての可能なデータ点を含む直径Λの球体

ここで、すべてのデータ点が「友好的(friendly)」、つまり近くにあり、それぞれが平均に与える影響は最大でもrであり、rはΛよりずっと小さいと仮定します。

しかし、DPを確保する従来の方法では、サンプリングされる可能性の低い「非友好的な(Unfriendly)」点を含む近隣のデータセットを考慮するために、Λに比例したノイズを加える必要があります。

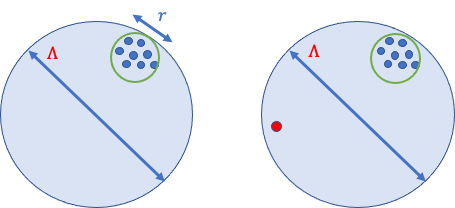
隣接する2つのデータセットで、1つの外れ値が異なっているケース
DPアルゴリズムでは、この外れ値を隠すために、各座標にΛに比例したノイズを加える必要があります。

ICML 2022で発表した「FriendlyCore: Practical Differentially Private Aggregation」では、差分プライベート集約(Differentially Private Aggregation)を計算するための汎用的なフレームワークを紹介しています。

FriendlyCoreフレームワークは、データを前処理して「Friendly」な部分(core)を抽出し、その結果、従来のDPアルゴリズムで見られたプライベート集約エラーを低減します。プライベート集約では、集約に悪影響を与える非フレンドリーなポイントを考慮する必要がないため、ノイズを減らすことができます。

平均化の例では、まずFriendlyCoreを適用して外れ値を除去し、集計ステップでr(Λではない)に比例するノイズを追加します。

課題は、全体的なアルゴリズム(外れ値除去＋集計)を差分プライベートにすることです。これにより、外れ値除去スキームが強いられる事になり、アルゴリズムが安定化します。1つのポイント(外れ値、または外れ値ではない)だけ異なる2つの隣接する入力は、同様の確率で任意の(Friendlyな)出力を生成するはずです。

FriendlyCoreフレームワーク

データセットがFriendlyとみなされるのはどのような場合でしょうか？

それは、必要な集約のタイプに依存します。集約時の感度、すなわち個々のデータポイントが集約された出力に与える影響が小さいデータセットを捕捉すべきです。

これを定式化することから始めます。例えば、集約が平均化である場合、Friendlyという言葉は、直径が小さいデータセットを捉えるべきです。

抽象化するために、点xとyが互いに「近い」場合に正となるfを用いて、友好度を定義します。例えば、平均化のアプリケーションでは、xとyはそれらの間の距離がrより小さい場合に「近い」事になります。私達は、点xとyのすべてのペアが、第3の点z(データ内にあるとは限りません)に共に近い場合、データセットはFriendlyであると言います。

FriendlyCoreの根底にある考え方はシンプルです。ある点xをコアに加える確率は、xに近い要素の数の単調で安定した関数です。特に、xが他のすべての点に近い場合、外れ値とはみなされず、確率1でコアに残すことができます。

第二に、集計に加えるノイズを少なくすることで、より弱いプライバシーの概念を満たすFriendly DPアルゴリズムを開発します。これは、cとc’の和がFriendlyであるような隣接するデータセットcとc’に対してのみ、集約の結果が似ていることが保証されることを意味する。

私達の主な定理は、上記の要件を持つフィルターによって生成されたコアに友好的なDP集約アルゴリズムを適用した場合、この構成は通常の意味での差分プライベートになることを示します。