1.Connect the Dots:差分プライバシーのより効率的なプライバシーコスト推定(1/2)まとめ
・差分プライバシーはプライバシーを保証した上で分析や機械学習を可能にする
・差分プライバシーでは個々のアルゴリズムを合成した際の特性が重要となる
・Connect-the-Dotsは合成後のプライバシーコストを理解するための有用なツール
2.Connect the Dotsとは?
以下、ai.googleblog.comより「Differential Privacy Accounting by Connecting the Dots」の意訳です。元記事の投稿は2022年12月20日、Pritish KamathさんとPasin Manurangsiさんによる投稿です。
アイキャッチ画像はstable diffusion 2.1のDreamBooth拡張をstable diffusionのアウトペインティングで更にサイズ拡張した画像で、プライバシーを確保した装いで外出をする風の谷在住のNさん
差分プライバシー(DP:Differential Privacy)は、ユーザーデータのプライバシーを数学的に保証した上でデータ分析や機械学習(ML:Machine Learning)を可能にするアプローチです。
DPは、あるアルゴリズムの「プライバシーコスト」、すなわち、与えられたデータセットに対して、ある一人のユーザーのデータを追加したり削除したりしても、そのアルゴリズムの出力分布が大きく変化しないことを保証し、その保証レベルを定量化するものです。
このアルゴリズムは、εとδという2つのパラメータで特徴付けられ、両者の値が小さいほど「よりプライベート」であることを示します。プライバシー保証枠(ε、δ)とアルゴリズムの実用性の間には自然な緊張関係があります。
プライバシー保証枠が小さいと、出力がより「ノイズ」になってしまい、予測が信頼できないためしばしば実用性が低くなってしまいます。したがって、DPの基本的な目標は、望ましいプライバシー保証枠で可能な限り多くの効用を達成することです。
DPの重要な特性は、プライバシーコストを理解する上でしばしば中心的な役割を果たす合成時(composition)の特性です。合成時の特性とはDPアルゴリズムの組み合わせを「単一のアルゴリズム」として見た場合に、正味のプライバシーコストを反映したものです。
代表的な例として、Differentially-Private stochastic gradient descent(DP-SGD)アルゴリズムが挙げられます。このアルゴリズムは、MLモデルを複数の反復で学習させますが、それぞれの反復が差分プライバシであるため、DPの合成特性を適用する必要があります。
DPの基本的な合成定理は、アルゴリズムの集合のプライバシーコストは、最大でもそれぞれのプライバシーコストの合計であることを述べています。しかし、多くの場合、これは全体的に見た際に過大評価となる可能性があります。いくつかの改良された合成定理は、合成によるプライバシーコストのより良い推定値を提供します。
2019年には、DPに基づく分析技術を開発者が利用できるように、オープンソースのDPライブラリをGitHub上で公開しました。本日、このライブラリに、合成のプライバシーコストを理解するための有用なツールであるConnect-the-Dotsを追加したことを発表します。Connect-the-Dotsは、プライバシー損失分布離散化に基づく新しいプライバシー会計アルゴリズムです。
このアルゴリズムは、PETS 2022で発表された論文「Connect the Dots: Tighter Discrete Approximations of Privacy Loss Distributions」をベースにしています。この会計アルゴリズムの主な新規性は、プライバシー損失分布のより正確な離散化を構築するために間接的なアプローチを使用することです。
私達は、Connect-the-Dotsが、精度と実行時間の点で、文献にある他のプライバシー会計手法よりも大きな利点をもたらすことを発見しました。また、このアルゴリズムは、最近、広告予測モデルの学習におけるDP-SGDのプライバシー保護に適用されました。
差分プライバシーとプライバシー損失分布
ランダム化アルゴリズムは、その出力が訓練データセットの任意の1つのエントリに「有意に依存しない」場合、DP保証を満たすと言われ、パラメータ(ε, δ)で数学的に定量化されます。
例えば、DP-SGDの動機となる例について考えてみましょう。プライベート保証なしの通常のSGDで学習させた場合、ニューラルネットワークは原理的に学習データセット全体を重みで符号化することができるため、学習済みモデルからいくつかの学習サンプルを復元することができます。一方、プライベート保証ありのDP-SGDで学習した場合、ある学習サンプルが自明でない確率で再構成できた場合、その学習サンプルが学習データセットに含まれていなくても再構成できることが公式に保証されます。
ホッケースティックダイバージェンス(hockey stick divergence)とは、εでパラメータ化され、下図に示すように2つの確率分布間の距離の尺度です。
DPアルゴリズムのプライバシーコストは、2つの確率分布PとQの間のホッケースティックダイバージェンスによって決定されます。
PとQの間のホッケースティックダイバージェンスの値が最大でもδであれば、アルゴリズムはパラメータ(ε, δ)でDPを満たします。
(P、Q)間のホッケースティックダイバージェンスは、\(δ_{P||Q}(ε)\)と表記され、\(PLD_{P||Q}\)と表記される関連プライバシー損失分布によって完全に特徴付けられます。
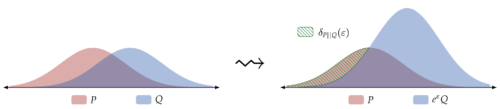
左:分布PとQの間のホッケースティックダイバージェンス\(δ_{P||Q}(ε)\)の図
右:これはPの確率質量が\(e^{ε}Q\)以上であることに対応し、ここで、\(e^{ε}Q\)はQの確率質量の\(e^ε\)スケーリングです
PLDを扱う主な利点は、アルゴリズムの構成が対応するPLDの畳み込みに対応することです。この事実を利用して、先行研究では、高速フーリエ変換アルゴリズムを用いて個々のPLDの畳み込みを行うだけで、個々のアルゴリズムの合成に対応するPLDを計算する効率的なアルゴリズムが設計されています。
しかし、多数のPLDを扱う場合の課題として、PLDが連続分布であることが多く、畳み込み演算が実際には困難であることが挙げられます。そこで研究者は、等間隔に配置された点を用いてPLDを近似する様々な離散化アプローチを適用することが多いです。例えば、プライバシーバケットアルゴリズムの基本バージョンでは、2つの離散化点の間の区間の確率質量は、完全に区間の高い方に割り当てられます。
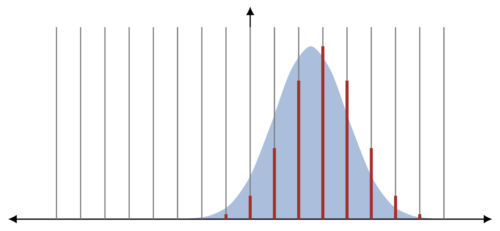
確率質量切り上げによる離散化の説明図
ここでは連続PLD(青)を、連続する点間の確率質量の切り上げにより、離散PLD(赤)に離散化しています。
3.Connect the Dots:差分プライバシーのより効率的なプライバシーコスト推定(1/2)関連リンク
1)ai.googleblog.com
Differential Privacy Accounting by Connecting the Dots
2)petsymposium.org
Connect the Dots: Tighter Discrete Approximations of Privacy Loss Distributions(PDF)
3)github.com
google / differential-privacy
4)www.youtube.com
[3B] Connect the Dots: Tighter Discrete Approximations of Privacy Loss Distributions



