量子コンピュータを使って理論検証ではなく新規発見を行う(2/2)

１．量子コンピュータを使って理論検証ではなく新規発見を行う(2/2)まとめ

・量子シミュレーションは理論予測の検証に使われることがほとんどであった
・今回は予測されていなかった現象を実験的調査で初めて発見する事ができた
・光子に「束縛状態」が存在し、それが予想外に堅牢である事を確認できた

２．結合状態が堅牢な理由

以下、ai.googleblog.comより「Formation of Robust Bound States of Interacting Photons」の意訳です。元記事は2022年12月8日、Alexis MorvanさんとTrond Andersenさんによる投稿です。

アイキャッチ画像はstable diffusion の生成

合唱団の一人一人が歌に貢献しているように、光子の進むべき道も光子の波動関数に貢献しているのです。最初は隣り合った場所に集まっていた光子の集団は、それぞれの光子が取りうるすべての経路の重ね合わせに発展していきます。

しかし、光子が隣の光子と相互に影響し合うと、そうはいかなくなります。ある光子が隣人から離れると、その位相の蓄積率が変化し、隣人との同期がとれなくなります。光子が離れる際の経路はすべて重なり合い、破壊的な干渉を引き起こします。合唱団がそれぞれ自分のペースで歌っているようなもので、歌そのものは洗い流され、個々の歌手の喧噪の中で聞き分けられなくなります。

さまざまな光子の配置が考えられる中で、唯一生き残る可能性があるのは、すべての光子が束縛状態(bound states)でまとまっている配置です。このように、相互作用は、光子が束縛していない他のすべての可能性を抑制することによって、束縛状態の形成を促進し、導くことができるのです。

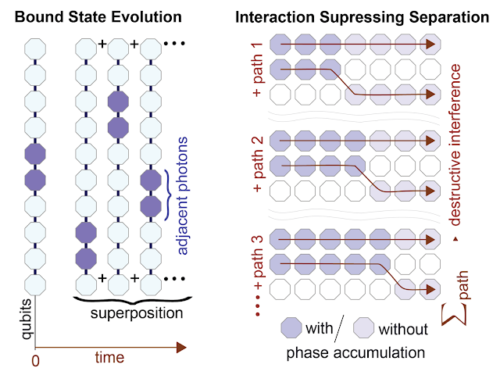
左：互いに影響しあって束縛状態を形成する光子の進化
右：時間は左から右へ進み、各経路は2光子の束縛状態を破ることができる経路の1つを表しています。相互作用により、これらの経路は破壊的に干渉し、光子が分裂するのを防ぎます。

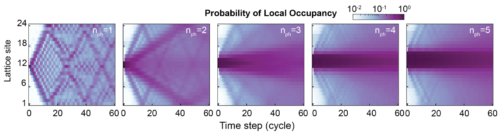
n個の光子の束縛状態のゲートサイクル(離散時間ステップ)に対する占有確率
様々な大きさの束縛状態を用意し、その変化を観察しました。その結果、大部分の光子(色の濃い方)が束縛されたままであることが分かりました。

このプロセッサでは、まず2個から5個の光子を隣接する敷地に置き(つまり、隣接する2個から5個の量子ビットを「1」に、残りの量子ビットを「0」に初期化)、それらがどのように伝搬するかを調べます。

まず、理論的に予測されるパラメータ領域では、両者はくっついたままであることに気づきました。次に、大きな束縛状態はリングの周りをゆっくりと動くことがわかり、「より重い」という事実と一致します。

上の図では、光子の初期位置に最も近い縦軸の12番の敷地が、束縛状態の光子の数(nph)が増えても他の敷地より暗いままであり、結合した光子の数が増えてもリングの周りをあまり伝わらないことを示しています。

束縛状態は単一の複合粒子のように振る舞う

結合状態が物理的に定義された単一の粒子として振る舞うことをより厳密に示すために、粒子のエネルギーが運動量によってどのように変化するか、すなわちエネルギー-運動量分散関係を測定する方法を考案しました。

束縛状態のエネルギーを測定するためには、2つの状態のエネルギー差が、その相対的な位相が時間とともにどれだけ速く成長するかを決定することを利用します。そこで、光子のない状態と重ね合わせた束縛状態を用意し、その位相差を時間・空間の関数として測定します。

そして、この測定結果を分散関係に変換するために、フーリエ変換を利用して、位置と時間をそれぞれ運動量とエネルギーに変換します。こうして、格子上の励起子のエネルギーと運動量の関係ができあがります。

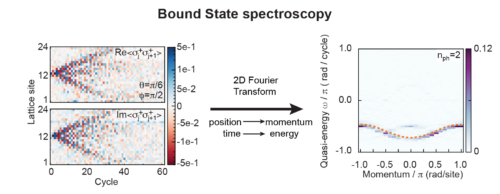
束縛状態の光子を分光法で測定
n個の光子の束縛状態と真空(光子なし)の位相蓄積を、敷地と時間の関数として比較。2次元フーリエ変換により、束縛状態の準粒子(quasiparticle)の分散関係を得ることができます。

可積分性を壊す

上記の系は「可積分(integrable)」であり、十分な数の保存量(conserved quantities)を持っているため、そのダイナミクスは利用可能な計算空間のごく一部に制約されることを意味します。

このような可積分領域では、束縛状態の出現はそれほど驚くべきことではありません。実際、似たような系で束縛状態が2012年に予測され、2013年に観測されました。

しかし、これらの束縛状態は壊れやすく、その存在は通常、可積分性に由来すると考えられています。しかし、より複雑な系では、対称性が乏しくなり、可積分性がすぐに失われてしまいます。そこで私たちは、可積分性を壊したときにどのように束縛状態が消えるかを調べ、その硬直性を理解しようと考えました。

可積分性を壊すには、どの量子ビットをfSimのゲートで接続するかを変更します。交互に配置されたサイトでは、2つの最近接敷地へのホップに加えて、リングから半径方向外側に配置された第3の敷地にもホップできるように、量子ビットを追加しました。

束縛状態は位相空間のごく一部に拘束されますが、可積分性の破れに伴うカオス的な振る舞いによって、系が位相空間をより自由に探索できるようになると期待されました。そうなれば、束縛状態はバラバラになるはずです。

しかし、そうではないことがわかりました。可積分性の破れが非常に強く、光子が隣接する2つのリング敷地のいずれかにホップするのと同じように第3サイトにホップする可能性がある場合でも、束縛状態はデコヒーレンス効果(decoherence effect)によってゆっくりと崩壊するまで、そのまま維持されます。(詳細は論文参照)。

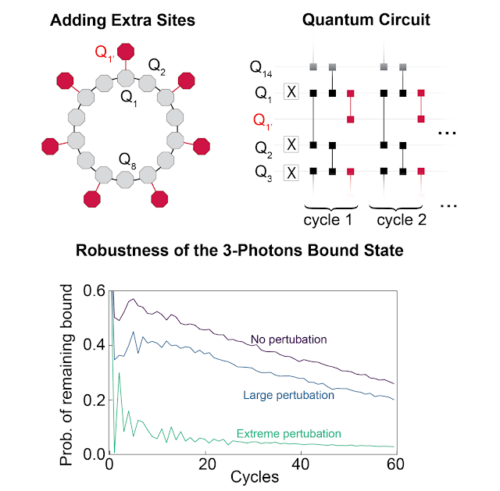
上：可積分性を破るための新しい配置
交互に配置された敷地は、半径方向外側に向いた第3の敷地に接続されています。これにより、システムの複雑さが増し、カオス的な振る舞いをする可能性があります。
下：このように複雑さが増すと、系は可積分性を超えてしまいますが、3光子束縛状態は比較的大きなユレ(摂動)に対しても安定なままであることがわかりました。束縛状態を維持する確率は、デコヒーレンスによってゆっくりと減少します(論文参照)

まとめ

この予想外の回復力について、私たちはまだ納得のいく説明を持っていません。この現象は「プレサーマル化(prethermalization)」と呼ばれるもので、系内のエネルギー規模が不釣り合いであるために、系が熱平衡に達するのが遅くなる現象に関係しているのではないかと推測しています。今後、さらに研究を進めることで、プレサーマル化と可積分性の関係を含む多体系量子物理学の新たな知見が得られると期待されます。