古典的アルゴリズムと量子アルゴリズムを組み合わせて量子モンテカルロ法を実現(3/3)

１．古典的アルゴリズムと量子アルゴリズムを組み合わせて量子モンテカルロ法を実現(3/3)まとめ

・古典的コンピュータと量子コンピュータの分業で両方のリソースを有効に活用できた
・過去最大規模の16量子ビットを使ってダイヤモンド結晶中の炭素のエネルギーを計算できた
・量子コンピュータで作成したデータを使って古典的なモンテカルロ手法に持ち込む事ができる

２．16個量子ビットを使った計算

以下、ai.googleblog.comより「Hybrid Quantum Algorithms for Quantum Monte Carlo」の意訳です。元記事は2022年3月16日、William J. Hugginsさんによる投稿です。

アイキャッチ画像のクレジットはPhoto by Mark de Jong on Unsplash

このように古典的コンピュータと量子コンピュータで分業することで、両方のリソースを有効に活用することができました。

Sycamore量子プロセッサーを使って、古典的なコンピュータを使った方法では規模拡大が困難な基底状態への近似を準備しました。量子プロセッサーを数時間使うだけで、古典計算機でモンテカルロ法を実行するのに必要なデータをすべて抽出することができました。

このデータは、現在の量子計算と同様にノイズが多いものでしたが、十分な信号が得られていたため、古典計算機を用いて、真の基底状態を非常に正確に再現することができました。(下図参照)

実際、量子コンピュータで基底状態の低分解能近似値(電子の位置を数個の量子ビットで符号化)を用いた場合でも、古典コンピュータははるかに高い分解能(電子の位置がより現実に即した形)で効率的に解けることが示されたのです。

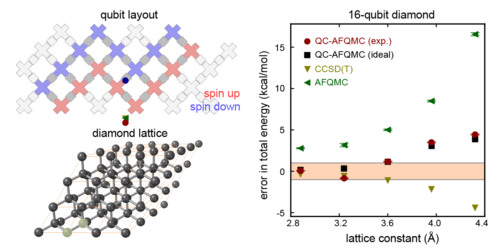
左上：今回の最大の実験に使用した16個の量子ビットを示す図
左下：ダイヤモンド結晶中の炭素原子の説明図。2つの原子に着目して計算を行いました(半透明の黄色でハイライトされている2つ)
右図：格子定数(lattice constant、2つの炭素原子の間隔)を調整すると、全エネルギーの誤差(ゼロに近いほど良い)がどのように変化するかを示した図
結晶の構造など、私たちが気にかける多くの性質は、原子を移動させたときにエネルギーがどのように変化するかを理解することで決定することができます。
量子コンピュータを使って行った計算(赤い点)は、2つの最先端の古典的手法(黄色と緑の三角形)と同等の精度で、ノイズの多い量子コンピュータではなく、完全な量子コンピュータを使った場合に得られるであろう数値(黒い点)に極めて近いものでした。この赤と黒の点が非常に近いということは、量子コンピュータのノイズに圧倒されたのではなく、量子コンピュータで単純すぎる近似基底状態を使ったために、計算の誤差が生じたことを物語っています。

新しいハイブリッド量子アルゴリズムを用いて、化学や材料科学の分野で過去最大規模の量子計算を行いました。16量子ビットを使って、ダイヤモンド結晶中の2つの炭素原子のエネルギーを計算したのです。

この実験は、私たちが初めてScamoreを使って行った化学計算よりも4量子ビット多く、より正確な結果が得られ、基礎となる物理のより良いモデルを使用することができました。量子コンピュータのデータを使って強力な古典モンテカルロ計算を導くことで、ノイズに対して本質的に堅牢な方法で計算を行うことができました。

私たちは、この新しい研究の方向性について楽観的であり、この種の計算を古典的な計算でできる限界まで拡大し、さらには研究が困難な世界の隅々まで拡大するという挑戦に胸を躍らせています。私たちの前にある道は長いですが、私たちの道具箱の中に新たな道具が増えたことに興奮しています。

謝辞

この原稿の共著者であるBryan O’Gorman, Nicholas Rubin, David Reichman, Ryan Babbush、そして特にJoonho Leeの多くの貢献と、実験実行を手伝ってくれたCharles Neill、Pedram Roushamに感謝します。また、Sycamoreプロセッサの設計、構築、プログラミング、校正を行ったGoogle Quantum AIチームにも感謝したいと思います。