オームの法則を使って代替経路問題を解く(2/2)

１．オームの法則を使って代替経路問題を解く(2/2)まとめ

・電流を求めるにはキルヒホッフの法則とオームの法則を用いて電圧に関する方程式を解く
・方程式を高速で解くためにガウスの消去法を使って回路をシンプルに変換する
・ボトルネックを特定する事でネットワークの電気的な流れを簡単に計算できる事が可能

２．ガウスの消去法

以下、ai.googleblog.comより「Robust Routing Using Electrical Flows」の意訳です。元記事は2022年2月18日、Ali Kemal SinopさんとKostas Kolliasさんによる投稿です。

アイキャッチ画像のクレジットはPhoto by Enq 1998 on Unsplash

電気の流れを計算するために、キルヒホッフの法則とオームの法則をそれぞれ使います。

1)各交差点における電流の代数和はゼロに等しい
つまり、どの交差点に入る交通量もそこから出ることになります(例えば、3台の車がある通りから交差点に入り、別の車が別の通りから同じ交差点に入る場合、合計4台の車が交差点から出る必要があります)

2)電流は端点間の電圧差に正比例する
この式を書き下すと、各交差点の電位(つまり電圧)に対応するn個の変数を持つn個の方程式からなる連立一次方程式になります。電圧は道路網と直接の関係はありませんが、電流の流れを計算することで、前述のように代替路を探すのに役立ちます。

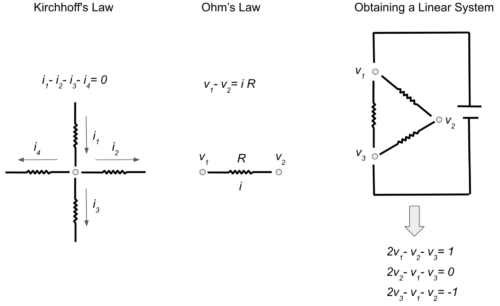
各電線に流れる電流i(または流量)を求めるには、キルヒホッフの法則とオームの法則を用いて、電圧(または電位)vに関する連立方程式を求めればよいです。このとき、3つの方程式(キルヒホッフの法則)と3つの未知数(各交点の電圧)からなる連立方程式が得られます。

そして、この連立一次方程式の変数の値を計算する際には、ラプラシアン行列(Laplacian matrix)という非常に特殊な行列を使うことになるのです。

このような行列は多くの有用な特性を持っています。例えば、対称的であり、疎ら(sparse)です。ゼロでなく、対角でもない項目の数はエッジの数の2倍に等しくなります。

このような連立一次方程式を線形に近い時間で解く解法は数多く存在しますが、低遅延でルーティング要求に素早く応答するという目的には、まだ遅すぎます。そこで私達は、道路網という特殊なケースにおいて、これらの線形方程式系をより高速に解く新しいアルゴリズムを考案しました。

電気の流れを高速に計算

この新しいアルゴリズムの最初の重要な部分は、おそらく線形システムを解くための最もよく知られた方法であるガウスの消去法(Gaussian Elimination)を使う事です。

これは、ある抵抗ネットワークに対応するラプラシアン行列に対して実行されると、Y-Δ変換(ワイ-デルタ変換、Y字型の回路を三角型の回路と等価になるように変換する手法)に対応し、電圧を維持したままノードの数を減らすことができます。唯一の欠点は、エッジの数が増加する可能性があり、線形システムの解がさらに遅くなることです。例えば、10個の接続を持つノードをY-Δ変換で削除した場合、システムは35個の新しい接続を持つことになります！

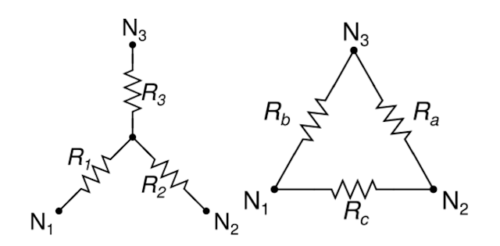
Y-Δ変換により、真ん中の交差部を取り除き、N1、N2、N3間の3つの接続(Ra、Rb、Rc)に置き換えることができます。(画像はWikipediaより)

しかし、ごく少数のノードでつながっている部分(これをボトルネックと呼びます)を特定し、ボトルネックのノードを残してそれ以外を消去していけば、最後にできる新しいエッジはボトルネックのノード間だけになります。

ボトルネックノードの数がY-Δで消去できるノードの数よりずっと少ない場合、つまり道路網の場合、橋やトンネルなどのボトルネックノードは通常の交差点よりずっと少ないので、これはグラフサイズに換算して大きな純減(例えば、100倍以上)となります。

幸いなことに、道路ネットワークにおけるこのようなボトルネックの特定は、ネットワークを分割することで容易に行うことができます。ボトルネック以外のノードにY-Δ変換を施すことで、電圧の解をより高速に求めることができる、より小さなグラフとなるのです。

しかし、ボトルネックノードがない残りの部分の電流の計算はどうでしょうか？

電流の有用な特性は、ボトルネックノードの電圧が分かれば、ネットワークの残りの部分の電気的な流れを簡単に計算できることです。ボトルネックを含まないネットワークの電気的な流れは、そのネットワークの残りのネットワークから分離するボトルネックノードの電圧にのみ依存します。

実際、小さな行列をあらかじめ計算しておけば、行列とベクトルの掛け算だけで電気的な流れを復元することができます。この行列は非常に高速で、並列に実行できます。

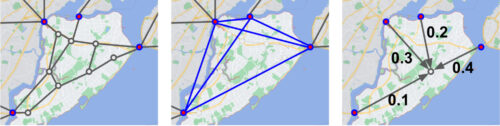
スタテン島(左)の道路ネットワークを考えてみましょう。この場合、電気的な流れを直接計算するのは時間がかかります。
橋(赤いノード)がボトルネックになっているので、ガウスの消去法(またはY-Δ変換)を繰り返し行うことで、島内の道路網をすべて消去することができます。その結果、ネットワーク(中央)はかなり小さなグラフになり、より高速な計算が可能になります。消去された部分の内部の電位は常にボトルネックノードの固定線形結合となります。(右)
モデルネットワークから電気の流れを与える解が得られたら、電気の流れが最も多くなるルートを観察し、道路ネットワークの代替ルートとして出力することができるのです。

結果

上記のアルゴリズムで計算された代替案を示す結果を以下に示します。

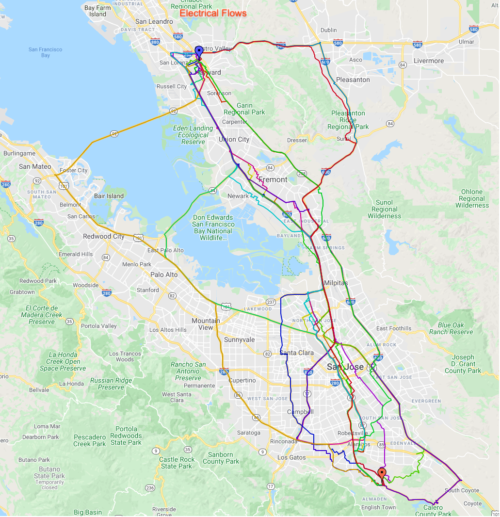
ベイエリアで見つかったさまざまな代替ルート
色の違いは、出発地(下側の赤いアイコン)から目的地(上側の青いアイコン)までの異なるルートに対応しています。

まとめ

この投稿では、道路ネットワークにおいて代替経路を計算する新しいアプローチについて説明しました。このアプローチは、この分野の数十年にわたる研究で適用されてきた主な手法とは根本的に異なり、電気回路の観点から問題を研究することにより、道路ネットワークにおける高品質の代替経路を提供するものです。このアプローチは、実用的なシステムにおいて非常に有用であることが証明されており、代替経路計算と関連する問題の分野でより多くの研究が行われることを期待しています。この研究の詳細については、下部リンクよりyoutubeのSIGSPATIAL 2021の講演記録をご覧ください。