道路網を効率的に分割して最短経路探索を高速化(1/2)

１．道路網を効率的に分割して最短経路探索を高速化(1/2)まとめ

・古典的なアルゴリズムは現在も大規模問題の解決に役立つことが良くある
・ランダムウォークを使用して北米大陸の道路網全体を高品質に分割できた
・同様の出力品質を持つ他の分割アルゴリズムよりもほぼ1桁速い速度で実行可能

２．道路網を分割して最短経路問題を高速化

以下、ai.googleblog.comより「Efficient Partitioning of Road Networks」の意訳です。元記事の投稿は2021年9月30日、Ali Kemal SinopさんとMahmuda Ahmedさんによる投稿です。

アイキャッチ画像はドイツのアウトバーンの立体交差でクレジットはPhoto by Alexander Schimmeck on Unsplash

古典的なアルゴリズムに基づいて解決を試みる手法は、旅行の旅程決定や電気自動車の目標地まで経路(ルーティング)問題の解決など、いくつかの大規模な問題に関する最近の革新に役立つことが証明されています。

たとえば、ダイクストラのアルゴリズム(Dijkstra’s algorithm)はグラフのルートを計算するためによく使用されます。しかし、必要になる計算量は小さな町の規模を超えると急速に大きくなる可能性があります。

ただし、道路網を「分割(partitioning)」するやり方であれば、計算中に検索されるグラフの量を効果的に縮小することが出来るので、アルゴリズムを大幅に高速化できます。

本投稿では、古典的なアルゴリズムのアイデアを使用して道路ネットワークのグラフ分割アルゴリズムを設計した方法について説明します。その一部は、WWW2021で「Sketch-based Algorithms for Approximate Shortest Paths in Road Networks」として紹介されています。

ランダムウォークを使用します。これは、直観に反していますが、ネットワークサイズを大幅に縮小することにより、最短ルートを計算する便利な古典的な概念です。私たちのアルゴリズムは、北米大陸の道路網全体の高品質な分割を、同様の出力品質を持つ他の分割アルゴリズムよりもほぼ1桁速い速度で見つけることができます。

グラフを使用した道路網のモデル化

道路網とグラフの間には、交差点がノードになり、道路がエッジになる、よく知られた便利な対応があります。

Wikipediaより引用した画像

ルート探索作業が分割からどのような利益を得るかを理解するために、最短ルートを見つけるための最もよく知られている解法である、幅優先探索方式で機能するダイクストラアルゴリズムを考えてみましょう。

ダイクストラアルゴリズムは、出発点からゴール地点を見つけるまで、徹底的な検索を実行します。このため、出発点とゴール地点間の距離が大きくなると、計算にかかる時間が桁違いに長くなる可能性があります。

たとえば、ワシントン州シアトルからカリフォルニア州サンフランシスコまでのルートよりも、ワシントン州シアトル内のルートを計算する方が高速です。

さらに、大都市圏内のルート探索の場合でも、計算中にダイクストラアルゴリズムによって探索される空間が膨大な量であれば、実用に耐えない数秒単位の遅延が発生します。ただし、内部の経路は多くても外部への経路が少ない領域(ニューヨーク州スタテンアイランドなど)の地域を特定すると、計算を複数の小さな塊に分割できます。

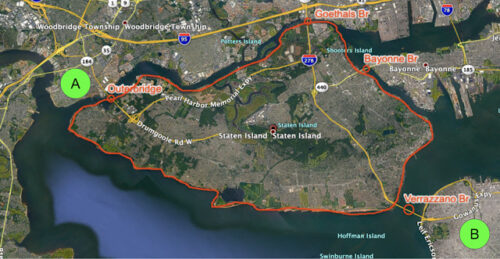
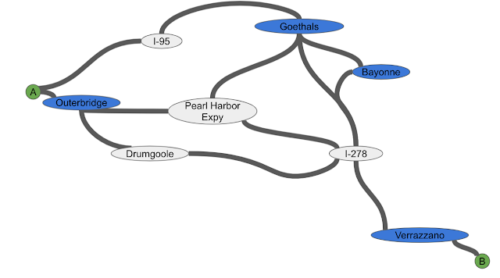
上：ニューヨーク州スタテンアイランド周辺のルーティング問題
下：グラフ問題として考えた際のパーティショニング。青いノードは、スタテンアイランドへの出入り口のみを示しています。

上の画像のポイントAからポイントBまで運転することを考えてみましょう。スタテンアイランドに入る場所(OuterbridgeまたはGoethals)と出る場所(Verrazzano)を決めると、問題は3つの小さな運転区間に分けられます。入口、出口、行き先(destination)です。行き先では利用可能な最適なルートを使用します。

つまり、ルーティングアルゴリズムは、これらの特別なポイントであるビーコン(beacons)を考慮するだけでポイントAとポイントBの間を移動できるため、最短経路をより速く見つけることができます。

ビーコンは、ビーコンの数が多すぎない場合にのみ有用であることに注意してください。ビーコンの数が少ないほど、追加する必要のあるショートカットが少なくなり、検索スペースが小さくなり、計算が高速になります。したがって、適切なパーティショニングを行うためには、コンポーネントの数(つまり、道路網の特定の領域)に対して比較的少ないビーコンを使用する必要があります。

スタテンアイランドの例が示すように、実際の道路網には多くのビーコン(橋、トンネル、峠などの特別なポイント)があります。

その結果、一部のエリアは非常に多くの接続があり(たとえば、大きな通りが格子状になっている)、他のエリアでは接続が多くありません(たとえば、2つの橋を介してのみアクセスできる)。問題は、コンポーネントを効率的に定義し、道路網を接続するビーコンの最小数を特定する方法になります。