PCR検査の効率を劇的に向上できるベイジアングループテスト(2/2)

１．PCR検査の効率を劇的に向上できるベイジアングループテスト(2/2)まとめ

・集団をスクリーニングして感染者を特定することはCOVID-19の流行で世界が直面している問題
・ベイジアン最適実験計画法は確率論的な考え方を採用し個人の感染確率を効率的に算出可能
・一部の個人が病原体を広めてしまう可能性が高いと思われるケースを検知でき効率的な対策が可能

２．ベイジアン最適実験計画法とは？

以下、ai.googleblog.comより「Exploring Faster Screening with Fewer Tests via Bayesian Group Testing」の意訳です。元記事の投稿は2020年7月14日、Marco CuturiさんとJean-Philippe Vertさんによる投稿です。

アイキャッチ画像のクレジットはPhoto by National Cancer Institute on Unsplash

ベイジアン最適実験計画法により少ないテストでより多くの人々をスクリーニング
私たちが提案する戦略は、探偵が事件を調査するように検査を行っていきます。

まず、これまでに実施されたすべてのテスト(既にテスト結果が存在する場合)の証拠と感染率に関して判明している事前情報を使用して、感染の有無についていくつかの仮説(a)を立てます。

これらの仮説を使用して、私達の探偵は可能な限り多くの仮説の真偽を確かめる事ができる可能性のある次のグループ(b)を生成し、もっともらしい仮説が調査ターゲットを明確に識別するために十分なほど小さくなるまで(a)と(b)をループします。

より正確には、

(a)
全人口をn人と想定すると、感染状態は長さnの２値ベクトルで表現できます。ここで感染者は1で表現し、非感染0で表現する事とします。

ある時点で、人口は特定の状態、つまり少数が感染者(すなわち1)でほとんどが非感染者(すなわち0)としてベクトル表現する事ができます。グループテストの目標は、できるだけ少ないテストを使用してこの状態を識別することです。

感染率に対して従来信じられてきている事(病気にかかっている人は比較的少数)と、これまでに観察されたテスト結果(もしテスト結果が存在する場合)から考えると、ごく一部の人のみが感染している状態がもっともらしいと予想されます。

2のn乗(nが小さい場合でも非常に大きい数になります)の全ての可能な状態について妥当性を評価するのではなく、逐次モンテカルロ法(SMC:sequential Monte Carlo)を使用して妥当性のある仮説をサンプリングする、より効率的な方法を使用します。

一般的にはかなり計算コストがかかりますが(私達の実験環境ではGPUを使用して数分程度)、本研究では、SMCサンプラーがnが大きくとも扱いやすいことを示し、グループテストの新しい可能性を開いています。

要するに、数分の計算コストと引き換えに、私達の探偵はこれまでに観察されたテスト結果を説明できるかもしれない数千の広範な仮説のリストを得る事ができます。

(b)
テスト結果に関する仮説のリストを得た私達の次の戦略は、探偵がそうするように、追加の証拠を選択的に収集することによって調査を進行します。

もし、次のループでk個のテストを実行可能な場合、私達の戦略では、ベイジアン最適実験計画のフレームワークを使用して計算されるk個の新しいグループをテストすることを提案します。

直感的に考えると以下のようになります。

k = 1の場合、つまり新しいグループを1つしかテストできない場合、現在の仮説を元に推測してもテスト結果がどうなるかわからないようなグループに対してテストする事には明らかな利点があります。つまり、現在の仮説セットから考えて、テスト結果が陽性となる確率が可能な限り50%に近いグループが望ましいグループとなります。

実際、調査を進めるには、新しいテスト結果によって提供されるサプライズファクター(または獲得情報量:Information Gain)を最大化するのが最善です。

このアイデアをk > 1個の新しいグループのセットに一般化するために、これらの「仮想グループテスト」と「仮説の分布」の相互情報量を計算することにより、このサプライズファクターにスコアを付けます。

また、仮説の分布を使用してこれらの新しいグループをテストすることで得られるROC曲線の下の予想面積(AUC:Area Under Curve)を計算する、より複雑なアプローチについても検討します。

これらの2つの基準が最も大きくなるように、貪欲法アプローチ(greedy approach)を使用します。その結果、2つのグループセレクター、GMIMAXおよびGAUCMAX(相互情報量の貪欲最大化またはAUC)が生成されます。

「テストを実行する実験(wet_lab)」と、「samplerおよびgroup_selectorで構成される私達の戦略」の相互のやりとりをオープンソースとして公開したパッケージ内で使われているクラス名を使用して次の図にまとめます。

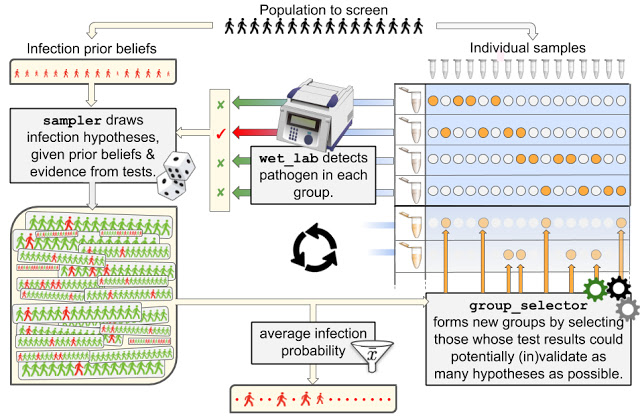
私たちのグループテストフレームワーク内での相互作用について説明します。

wet_labは、テスト結果を蓄えます。蓄えたテスト結果はsamplerが感染状態に関する何千ものもっともらしい仮説を構築するために使用されます。

これらの仮説は、真の感染状態を絞り込むためにはどのグループに対してテストをする事が最も効率的であるかを把握する最適化手順group_selectorによって使用されます。

新たなグループが形成されると、これらの新しいグループは再度テストされ、１ループが終了します。

任意の時点で、samplerによって形成された仮説を平均して、各患者の平均感染確率を取得できます。これらの確率から、患者が感染しているかどうかの決定は、信頼係数(confidence level)でこれらの確率をしきい値処理することによって行うことができます。

ベンチマーク
様々な設定(感染率(infection rates)、テストノイズレベル(test noise levels))で様々なベースラインに対して2つの戦略GMIMAXとGAUCMAXのベンチマークを行い、テスト数の増加に応じてパフォーマンスがどうなるかを調べました。シンプルなDorfman戦略に加えて、私達が比較対象としたベースラインには、非適応戦略の混合(origami assays, random designs)が含まれており、これらはいわゆる有益なドルフマンアプローチ(informative Dorfman approach)で後段階で補完されます。私達のアプローチは、全ての設定で他のアプローチを大幅に上回っています。

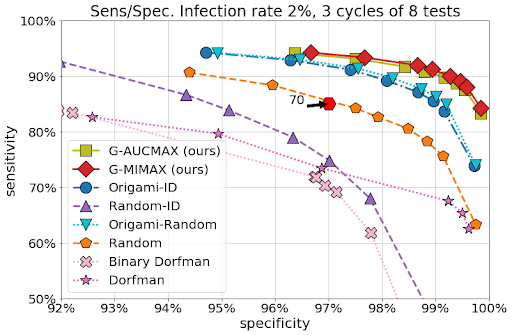
感染率2%の70人のサンプル母集団に対して5000回のシミュレーションを実行しました。
現在のPCRマシンの代表的な最大グループサイズである10を使用したテストで、感度/特異度の値を85%/97%と想定しています。この図は、適応型と非適応型の両方を比較対象とし、少なくとも24事例で(3サイクルで最大8つのテスト)で、私達のアプローチが他の比較対象よりも優れていることを示しています。個別テスト(赤い六角形、PCRテストが70回必要)よりも大幅にパフォーマンスが向上し、グループテストによって検査数が節約できる可能性を強調しています。その他の設定については、論文を参照してください。