1.モジュラーディープラーニング用の再帰的スケッチ(1/2)まとめ
・スケッチとはディープニューラルネットワークが入力をどのように処理しているかを要約する試み
・スケッチはニューラルネットワークに記憶を元にした回答や要約機能を持たせる事に繋がる
・複雑なネットワークであってもモジュール単位に分割されたモジュラーネットワークであれば適用可
2.スケッチとは?
以下、ai.googleblog.comより「Recursive Sketches for Modular Deep Learning」の意訳です。元記事の投稿は2019年9月10日、Badih GhaziさんとJoshua R. Wangさんによる投稿です。
従来の機械学習(ML)の多くは、利用可能なデータを利用してより正確な予測を行うことに焦点を当てています。
最近では、研究者は、アルゴリズムを小さく、効率的で、堅牢に設計する方法など、他の重要な目標を検討しています。これらのゴールを念頭に置くと、研究の目的は「エンコードされた情報を効率的に内部に保存できるニューラルネットワークシステムの設計」に行きつきます。
つまり、「複雑なディープネットワークが入力をどのように処理しているか?」について簡潔な要約(sketch:スケッチ)を計算する仕掛けです。スケッチは、Alon、Matias、およびSzegedyの基礎研究にまでさかのぼる豊富な研究分野であり、ニューラルネットワークが入力に関する情報を効率的に要約できるようにする研究です。
例えば、部屋に足を踏み入れ、部屋に存在する物体を一瞥する実験を想像してください。
現代の機械学習は、見た風景について、トレーニング時に知らされていた質問に答える事には優れています。「部屋には猫がいましたか?」「猫の大きさは?」
ここで、年間を通じて毎日この部屋を一瞥するとします。人間であれば、部屋を見た時間を思い出すことができます。「部屋にはどれくらいの頻度で猫がいましたか?」「普段あなたが部屋を見る時間帯は、朝でしたか?夜でしたか?」
このように、トレーニング時に設定さていない質問にも、記憶を元に質問に効率的に回答できる機械学習システムを設計する事ができるでしょうか?
ICML 2019で最近発表された「Recursive Sketches for Modular Deep Learning」では、機械学習モデルが入力をどのように理解するかを簡潔に要約する方法を探求しています。
私達はこれを、既存の(事前に訓練された)機械学習モデルを、その「スケッチ」に拡張し、スケッチを使用して記憶ベースの質問に効率的に回答することによって行います。
元の計算全体を保存するよりもはるかに少ないメモリを使用している事実にもかかわらず、例えば、イメージ間の類似性や要約統計などへの対応を実現します。
基本的なスケッチのアルゴリズム
一般に、スケッチアルゴリズムはベクトルxを元に、xのように動作するけれども、サイズががはるかに小さいアウトプットスケッチベクトルを生成します。
ストレージコストがはるかに小さいという事実により、ネットワークに関する情報を簡潔に保存できます。これは、メモリベースの質問に効率的に答えるために重要です。
最も単純な場合、線形スケッチxは、行列ベクトル積Axによって与えられます。ここで、Aは幅の広い行列です。つまり、つまり、列の数はxの元の次元に等しく、行の数は新しい縮小された次元に等しくなります。
このような変換手法は、大規模なデータセットにおける基本的なタスクを行うための、様々な効率的なアルゴリズムでも使われています。
基本的な統計(例えば、ヒストグラム、分位、四分位範囲)の推定、人気商品の特定(frequent elementsとして知られます)。又、個別の要素数(support sizeと呼ばれます)や、関連するノルム(ベクトル間の距離の概念)およびエントロピー(乱雑さ)の推定などです。
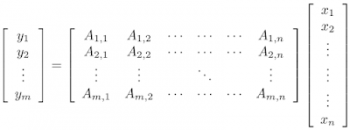
ベクトルxをスケッチする簡単な方法は、幅の広い行列Aを乗算して低次元ベクトルyを生成することです。
この基本的な変換アプローチは、データの重要な次元を単純に重みの大きさで識別することができる線形回帰のような比較的単純なケースでうまく機能します。(均一な分散状態であるという一般的な仮定の下で)
ただし、多くの最新の機械学習モデルは実際にはディープニューラルネットワークであり、高次元のembeddings(Word2Vec、Image Embeddings、Glove、DeepWalk、BERTなど)に基づいており、より困難です。しかしながら、これらのより複雑なネットワークの大部分のサブセットはモジュール式であるため、複雑さにもかかわらず、動作の正確なスケッチを生成できます。
3.モジュラーディープラーニング用の再帰的スケッチ(1/2)関連リンク
1)ai.googleblog.com
Recursive Sketches for Modular Deep Learning
2)arxiv.org
Recursive Sketches for Modular Deep Learning



コメント