1.偏微分方程式をより良く近似するために機械学習を利用(2/2)まとめ
・人間によるヒューリスティックな観察をニューラルネットワークに学習させる事が基本的アイディア
・ニューラルネットワークを従来のシミュレーション手法の要素と組み合わせる事で効率的な学習ができた
・これは機械学習と物理学を効果的に組み合わせる方法についての洞察に繋がる
2.機械学習と物理学を効果的に組み合わせる方法とは?
以下、ai.googleblog.comより「Learning Better Simulation Methods for Partial Differential Equations」の意訳です。元記事は2019年7月23日、Stephan Hoyerさんによる投稿です。
課題は、可能な限り最も粗いグリッドを使用しながら、高精細度シミュレーションの精度を維持することです。
私達が行った研究は、深い洞察に基づいた人間によるヒューリスティックな観察(例えば、「偏微分方程式の解は常に不連続性関数より滑らかにならなければならない」)を機械学習に基づく最適化されたルールで置き換えることです。これにより既存のスキームを改善できます。
MLモデルがこれを実現するために用いているルールは複雑であり、私達も完全には理解していません。しかし、それらは「風上」のような洗練された物理的原理をアイデアに組み込んでいます。流体の流れの中であなたに向かってくるものを正確にモデル化するためには、あなたは風が吹いている方向の上流を見るべきなのです。
単純な流体力学モデルの結果の例を以下に示します。
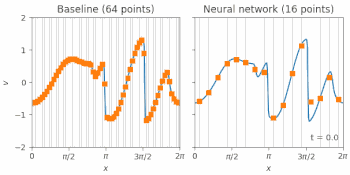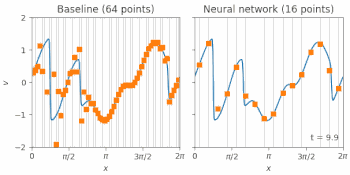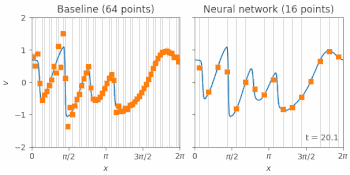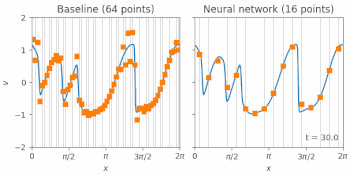
流体中の衝撃波のモデルであるバーガース方程式(Burgers equation)のシミュレーションは、標準的な有限体積法(FVM:finite volume method)(左図)、又は私達のニューラルネットワークベースの方法(右図)のいずれかで解を求める事ができます。
オレンジ色の四角形は、各手法を低解像度グリッド上にシミュレーションした結果を表しています。これらの点は、各タイムステップでモデルにフィードバックされ、次にそれらがどのように変化するかを予測します。青い線は、トレーニングに使用された正確なシミュレーションを示しています。 オレンジ色の四角が青い線を滑らかに描いていることからもわかるように、ニューラルネットワークによる解決法は、4倍粗いグリッドでも従来手法よりはるかに優れています。
私たちの研究はまた、機械学習と物理学を効果的に組み合わせる方法について、より幅広い教訓を示しています。ニューラルネットワークに物理世界の原理原則をゼロから習得させるのではなく、従来のシミュレーション手法の要素(既知の形式の方程式や有限体積法など)と組み合わせたのです。
これは、運動量保存の法則などの物理法則が、従来のシミュレーション手法内に構造的に保持されている事を意味します。それは、私たちの機械学習モデルが、これらの法則が最も良く当てはまるようなルールを集中して学習する事を可能にし、複雑な高次元空間でも法則を補間するような最適なルールを学ぶ事ができたのです。
次のステップ
私達は、天気予報や気候予報など、現実の影響を伴う大規模シミュレーション問題を解決するために、このホワイトペーパーで概説した手法をスケールアップすることに焦点を当てています。私達は、機械学習を科学計算の複雑なアルゴリズムに融合させることの大きな可能性に興奮しています。
謝辞
共著者のYohai Bar-Sinari、Jason Hickey、そしてMichael Brennerに感謝します。また、Google社内のの協力者であるPeyman Milanfar、Pascal Getreur、Ignacio Garcia Dorado、Dmitrii Kochkov、Jiawei Zhuang、そしてAnton Geraschenkoにも感謝します。
3.偏微分方程式をより良く近似するために機械学習を利用(2/2)関連リンク
1)ai.googleblog.com
Learning Better Simulation Methods for Partial Differential Equations
2)www.pnas.org
Learning data-driven discretizations for partial differential equations



コメント