1.データの力で古典的機械学習が量子機械学習を凌駕(1/2)まとめ
・量子コンピューターの優位性は通常、計算速度の速さとして語られる事が多い
・量子機械学習では利用できるデータの量も優位性の有無に影響を与える
・機械学習における量子優位性の問題を分析し優位性が発揮される場面を調査した
2.量子機械学習の優位性とは?
以下、ai.googleblog.comより「Quantum Machine Learning and the Power of Data」の意訳です。元記事は2021年6月22日、Jarrod McCleanさんとHsin-Yuan (Robert) Huangさんによる投稿です。
量子コンピューターの知識と機械学習の知識の両方が前提(そんな人は果たして世界中に何人いるのだろうかとは思う)のかなり難しいお話なので、飛ばし読み推奨ですが、超要約すると以下です。
量子コンピューターを使用すると、従来型のembeddingとは異なる形状を持つ量子embeddingを作成する事が出来て、量子embeddingが量子機械学習の優位性の源なのだけれども、量子embeddingを選択的に従来型のembeddingに投影すると、利用できるデータが十分に多いと従来型のembeddingが量子embeddingを凌駕するケースがある事がわかりました。
量子コンピューターは理論ではなく応用方法を探る段階に突入しているんだなぁ、との思いが更に強まりますね。パワーの投影をイメージしたアイキャッチ画像のクレジットはPhoto by Jaanus Jagomägi on Unsplash
量子コンピューティングは、近年、理論と実践の両方で急速に進歩しており、実用アプリケーションへの潜在的な影響への期待が高まっています。重要な関心領域の1つは、量子コンピューターが機械学習にどのように影響するかです。
私たちは最近、量子コンピューターが、従来型の、または「古典的な」コンピューターでは解決が難しい入力データ間で複雑な相関関係を持つ特定の問題を解決できることを実験的に示しました。
これは、量子コンピューターで作成された学習モデルが、アプリケーションにとって劇的に強力であり、より高速な計算、より少ないデータでのより良い一般化、またはその両方を誇る可能性があることを示唆しています。したがって、このような「量子超越性(quantum advantage)」がどのような状況で達成されるかを理解することは非常に興味深いことです。
量子超越性の概念は、通常、計算上の利点の観点から表現されます。つまり、入力と出力が明確に定義されたタスクがある場合、量子コンピューターが、同等の実行時間で従来の古典的マシンよりも正確な結果を達成できるか否かです。
大きな素数の積を因数分解するための「ショアの因数分解アルゴリズム(Shor’s factoring algorithm、RSA暗号化に関連)」や量子システムの量子シミュレーションなど、量子コンピューターが圧倒的な利点を持っていると考えられるアルゴリズムは数多くあります。
ただし、問題を解決することの難しさ、つまりは量子コンピューターの潜在的な利点は、データの可用性によって大きく影響を受ける可能性があります。そのため、量子コンピューターが機械学習タスクに役立つ場合を理解するには、タスクだけでなく、利用可能なデータにも依存します。量子コンピューターの利点を完全に理解するには、両方を含める必要があります。
Nature Communicationsに掲載された論文「Power of data in quantum machine learning」では、機械学習における量子優位性の問題を分析して、どのような時に適用すると優位性が発揮されるかをよりよく理解しようとします。
問題の複雑さがデータの可用性によって形式上どのように変化するか、そしてこの可用性が古典的な学習モデルに量子アルゴリズムに匹敵するレベルの力をどのように持たせるかを示します。
次に、スクリーニングを行うための実用的な手法を開発します。カーネル法で選択したデータembeddingsのセットに量子的利点があるか否かをスクリーニングする事を想定します。
スクリーニング手法と学習境界(learning bounds)に関する洞察を使用して、量子コンピューターで作成した特徴マップの特定の側面を古典的コンピューターの空間に投影する新しい手法を紹介します。
これにより、量子アプローチに古典的な機械学習から得た追加の洞察を吹き込むことができます。これは、これまでの量子学習の実験に基づいた最高の利点を示しています。
データの計算力
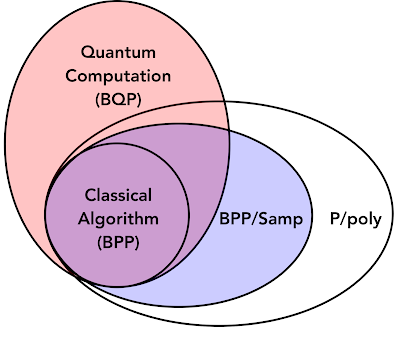
従来のコンピューターに対する量子優位性の考え方は、計算の複雑さの観点から論じられる事がよくあります。多数の因数分解や量子システムのシミュレーションなどの例は、有界量子多項式(BQP:bounded quantum polynomial)時間問題として分類されます。これは、古典的なシステムよりも量子コンピューターで処理しやすいと考えられている問題です。従来のコンピューターで簡単に解決できる問題は、有界確率多項式(BPP:Bounded Probabilistic Polynomial)問題と呼ばれます。
私達は量子過程(核融合や化学反応など)から得たデータを備えた学習アルゴリズムが、新しい問題(BPP/Sampと呼んでいます)を形成することを示します。
これは、データのない従来のアルゴリズムでは不可能ないくつかのタスクを効率的に実行でき、多項式サイズの関数で効率的に解決できる問題(P/poly)の一部です。これは、一部の機械学習タスクでは、量子の利点を理解するには、利用可能なデータも調べる必要があることを示しています。
幾何テストで量子機械学習の利点を確認
データの入手可能性に応じて利点の可能性が変化するという考察から、実務家は自分たちの問題が量子コンピューターに適しているかどうかを迅速に評価する方法を尋ねることができます。
これを支援するために、カーネル学習フレームワーク内での利点の可能性を評価するためのワークフローを開発しました。 私たちはいくつかのテストを調べましたが、その中で最も強力で有益なのは、私たちが開発した新しい幾何テスト(geometric test)でした。
量子ニューラルネットワークや量子カーネル法などの量子機械学習では、量子プログラムはしばしば2つの部分に分けられます。
「データの量子埋め込み(quantum embedding of the data、量子コンピューターを使用した特徴表現空間のembedding)」および「embeddingデータに適用される関数の評価」です。
量子コンピューターを使った量子カーネル法は従来のカーネル法を利用しますが、量子コンピューターを使用して、古典的なembeddingとは異なる形状を持つ量子embedding上のカーネルの一部またはすべてを評価します。
量子超越性の利点は、量子embeddingから生じる可能性があると推測されており、これは、現在利用可能な古典的な形状(geometry)よりも特定の問題にはるかに適している可能性があります。
特定の量子embedding、カーネル、およびデータセットをさまざまな従来のカーネルとすばやく比較するために使用できる、迅速で厳密なテストを開発しました。そして、全体に量子超越性の機会があるかどうかを評価します。たとえば、画像認識タスクに使用されるようなラベル関数などにです。
また、データ量を定量化する幾何定数g(geometric constant g)を定義します。gは幾何テストに基づいて、量子機械学習と従来型機械学習のギャップを理論的に埋めることができるデータの量です。これは、データの制約に基づいて、量子ソリューションが特定の問題に適しているかどうかを判断するための非常に便利な手法です。
3.データの力で古典的機械学習が量子機械学習を凌駕(1/2)関連リンク
1)ai.googleblog.com
Quantum Machine Learning and the Power of Data
2)www.nature.com
Power of data in quantum machine learning



