超並列グラフ計算：理論から実践へ(2/2)

１．超並列グラフ計算：理論から実践へ(2/2)まとめ

・AMPCモデルを使用して、実用的で効率的な実装に触発された理論的フレームワークを構築
・優れた実証的パフォーマンスと障害耐性を維持する新しい理論的アルゴリズム
・グラフのサイズに関係なく、最大マッチング、最大独立集合などを一定回数で発見可

２．超並列グラフ計算の実装

以下、ai.googleblog.comより「Massively Parallel Graph Computation: From Theory to Practice」の意訳です。元記事の投稿は2021年3月18日、Jakub ŁąckiさんとVahab Mirrokniさんによる投稿です。

アイキャッチ画像のクレジットはPhoto by Jonathan Pendleton on Unsplash

適応型超並列計算モデル
このアプローチを他の問題に拡張するために、DHTを利用するアルゴリズムを理論的に分析するモデルを開発することから始めました。結果として得られるAMPCモデルは、確立されたMPCモデルに基づいて構築され、分散ハッシュテーブルの使用によってもたらされる機能を正式に描写します。

MPCモデルには、同期ラウンドでのメッセージパッシングを介して通信するマシンのコレクションがあります。1つのラウンドで送信されたメッセージは、次のラウンドの開始時に配信され、そのラウンドの入力全体を構成します。(つまり、各マシンは1つのラウンドから次のラウンドに情報を保持しません)

最初のラウンドでは、入力がマシン全体にランダムに分散されていると想定できます。目標は、各ラウンドのマシン間の負荷分散を確保しながら、計算ラウンドの数を最小限に抑えることです。

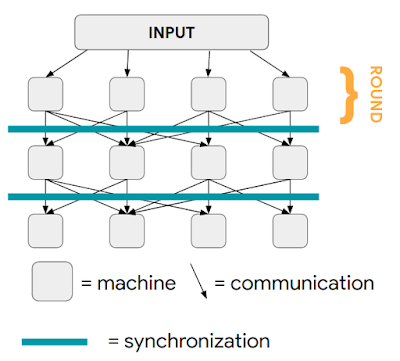
MPCモデルで行われる計算
各列は、後続の計算ラウンドで1台のマシンを表します。全てのマシンが計算ラウンドを完了すると、そのラウンドで送信されたすべてのメッセージが配信され、次のラウンドが開始されます。

次に、新しいアプローチを導入して、AMPCモデルを形式化しました。ここではマシンは、メッセージを介して通信する代わりに、ラウンド毎に書き込み専用の分散ハッシュテーブルに書き込みます。

新しいラウンドが開始されると、前のラウンドのハッシュテーブルが読み取り専用になり、新しい書き込み専用の出力ハッシュテーブルが使用可能になります。

重要な事は、通信方法のみが変更されることです。通信量とマシン毎の使用可能なスペースは、MPCモデルとまったく同じ方法で制限されます。従って、高レベルで考えると、AMPCモデルで追加された機能は、各マシンが一方的にデータの一部を与えられるのではなく、読み取るデータを選択できることです。

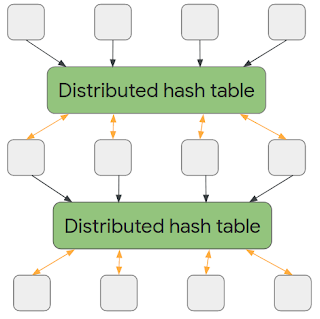
AMPCモデルで行われる計算
全てのマシンが一連の計算を完了すると、それらが生成したデータは分散ハッシュテーブルに保存されます。次のラウンドでは、各マシンはこの分散ハッシュテーブルから任意の値を読み取り、新しい分散ハッシュテーブルに書き込むことができます。

アルゴリズムの実証的評価
マシンの通信方法におけるこの一見小さな違いにより、多くの基本的なグラフの問題に対してはるかに高速なアルゴリズムを設計することができました。特に、論文「Parallel graph algorithms in constant adaptive rounds: theory meets practice」では、グラフのサイズに関係なく、連結成分、最小全域木、最大マッチング、最大独立集合を一定のラウンド数で見つけることができることを示しました。

AMPCアルゴリズムの実際の適用性を調査するために、Flume C ++(Flume JavaのC ++対応物)をDHT通信レイヤーと組み合わせてモデルを実体化しました。最小スパニングツリー、最大独立集合、最大マッチングについてAMPCアルゴリズムを評価し、DHTを使用しなかった実装よりも最大7倍のスピードアップを達成できることを確認しました。同時に、AMPCの実装では、完了するのに平均で10分の1のラウンドを使用し、ディスクに書き込むデータも少なくなりました。

AMPCモデルの実装では、ハードウェアアクセラレーションによるリモートダイレクトメモリアクセス(RDMA:Remote Direct Memory Access)を利用しました。これは、ローカルマシンのメモリからの読み取りよりもわずかに1桁遅い、数マイクロ秒の遅延でリモートマシンのメモリからの読み取りを可能にするテクノロジです。

一部のAMPCアルゴリズムは、対応するMPCアルゴリズムよりも多くのデータを通信しましたが、ディスクへのコストのかかる書き込みではなく、RDMAを使用してほとんど高速の読み取りを実行したため、全体的に高速でした。

結論
AMPCモデルを使用して、実用的で効率的な実装に触発された理論的フレームワークを構築しました。優れた実証的パフォーマンスが提供可能で、優れた障害耐性を維持する新しい理論的アルゴリズムを開発しました。AMPCモデルがすでに更なる研究の対象になっていることを嬉しく思い、AMPCモデルまたはその実際の実装を使用して他のどのような問題をより効率的に解決できるかを学ぶことに興奮しています。

謝辞
このブログ投稿で取り上げられている2つの論文の共著者には、Soheil Behnezhad, Laxman Dhulipala, Hossein Esfandiari, そしてWarren Schudyが含まれます。また、Graph Miningチームのメンバーのコラボレーション、特にMohammad Hossein Bateni のこの投稿への加筆に感謝します。規模拡大可能なグラフアルゴリズムに関する最近の研究の詳細については、neurips 2020で行われたGraph Mining & Learningに関するワークショップのビデオをご覧ください。