Performers：Attentionの規模拡大を容易にする(2/3)

１．Performers：Attentionの規模拡大を容易にする(2/3)まとめ

・通常のAttentionは保存されたAttention行列に入力された値を乗算して最終結果を取得
・Attention行列を分解すれば通常のAttentionメカニズムの結果を近似する事が可能
・FAVOR+はこの行列の結合性を利用して高速且つ効率の良いAttentionを実現

２．FAVOR+とは？

以下、ai.googleblog.comより「Rethinking Attention with Performers」の意訳です。元記事の投稿は2020年10月23日、Krzysztof ChoromanskiさんとLucy Colwellさんによる投稿です。

カーネル法やRandom FeaturesはBefore Deep Learning時代からある機械学習手法なので、深堀したい方は、Deepじゃない時代の機械学習本を読むと良いと思います。

例えば「埼玉県人」と「埼玉県人でない人」を線を引いて分けたいとします。埼玉に来ている他県人も他県に行っている埼玉県人もいるでしょうからそのままではシンプルな線は引く事は出来ませんが、仮に「埼玉県人」を全員上空100メートルにぶん投げる事が出来たら、空中に線をピッっと引いて分ける事ができます。このように次元を強引に増やして分離しやすくするのがカーネル法のアイディアです。しかし、カーネル法も埼玉県人の数が増えると計算量が指数関数的に増えてしまう弱点があるので、計算は厳密でなくても良いので近似しようってのがRandom Featuresのアイディアです。(すいません、埼玉県人に恨みはないです。映画「翔んで埼玉」の影響です。それと、この空中ぶん投げ解説はどなたかが書いていた話で私のオリジナルではありませんが、どこで読んだか失念してしまいました、重ねてすいません。)

アイキャッチ画像のクレジットはPhoto by Marine Golfetto on Unsplash

一般的なAttention
元のAttentionメカニズムでは、行列の行と列にそれぞれ対応するクエリとキーの入力があり、乗算され、softmax演算を通過して、アテンション行列が形成され、類似性スコアが格納されます。

この手法では、クエリとキーの積を非線形なソフトマックス操作に渡すので、その後、元のクエリとキーに分解する事ができないことに注意してください。

ただし、Attention行列を分解して、元のクエリとキーのランダムな非線形関数の積に戻すこともできます。これは、Random Featuresとも呼ばれ、類似性情報をより効率的にエンコードできます。

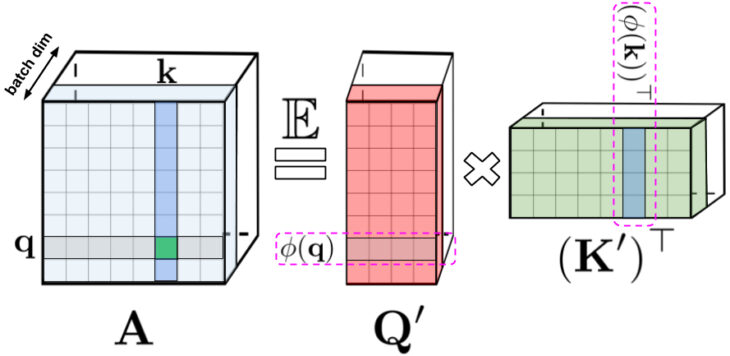
左側：標準的なAttention行列
これには、クエリとキーに対するソフトマックス操作によって形成された、入力の全てのペアの全ての類似性スコアが含まれており、qとkで示されます。
右側：標準のAttention行列は、下位の行列Q’およびK’を介して近似できます。元のクエリ/キーを潜在的にランダムな非線形関数(potentially randomized nonlinear functions)でエンコードする事でこれを行います。通常のsoftmax-attentionの場合、変換は非常にコンパクトであり、指数関数とランダムなガウス射影が含まれます。

通常のsoftmax-attentionは、指数関数とガウス射影によって定義されるこれらの非線形関数の特殊なケースと見なすことができます。

逆方向に推論もできることに注意してください。より一般的な非線形関数を最初に実装し、クエリ/キーの積で他のタイプの類似性測定値またはカーネルを暗黙的に定義する事でこれが可能になります。

カーネル法の従来の研究に基づいて、これを一般的なAttentionとして組み立てます。ほとんどのカーネルには閉じた形の式(closed form formula、有限数の標準的な演算を使用して表現される数式)は存在しませんが、それらに依存しないため、私達のメカニズムは引き続き適用できます。

私たちの知る限り、Random Featuresを使用してTransformerを実装した実際のアプリケーションでAttention行列を効果的に近似できることを示した研究はこれが初めてです。

これを可能にする新しいメカニズムは、正のRandom Featuresの使用です。つまり、元のクエリとキーの正の値の非線形関数です。これは、トレーニング中の不安定性を回避するために重要であり、通常のsoftmax-attentionメカニズムのより正確な近似を提供します。

FAVOR+に向けて：行列の結合性を利用した迅速なAttention
前述の分解を行う事により、暗黙のAttention行列を指数関数ではなく1次関数的に増加していくようにメモリを抑える事ができます。この分解を使用して、線形な時間でAttentionメカニズムを実施する事もできます。

元のAttentionメカニズムは、保存されたAttention行列に入力された値を乗算して、最終結果を取得します。Attention行列を分解すれば、二次元のAttention行列を明示的に作成しなくても、行列の乗算を組み替えて、通常のAttentionメカニズムの結果を近似することができます。

この原理が最終的にFAVOR+につながります。

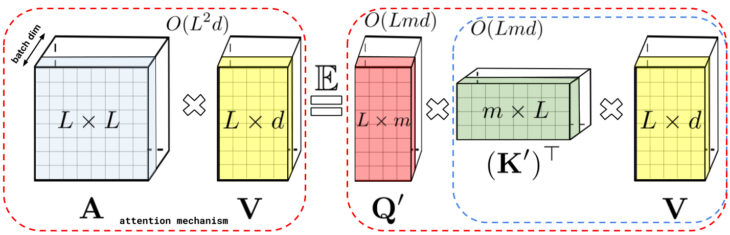
左：標準的なAttentionモジュールの計算
Attention行列Aと値テンソルVを使用して行列の乗算を実行することにより、最終的な結果が計算されます。
右：行列Aを低位に階数分解する事で得られる行列Q’とK’に分離し、破線で示される順序で行列の乗算を実行することにより、線形なAttentionメカニズムが得られ、Aまたはその近似を明示的に構築する必要がなくなります。

上記の分析は、いわゆる双方向Attentionに適しています。つまり、過去と未来の概念がない非因果的なAttentionです。

トークンが入力シーケンスの後半に表示される他のトークンに対応しない、一方向な(causal、因果的な)Attentionの場合、プレフィックス合計計算(prefix-sum computations)を使用するようにアプローチを少し変更します。

これは、通常のAttention行列のように明示的に下半分の三角行列を格納するのではなく、行列計算の現在の合計のみを格納します。

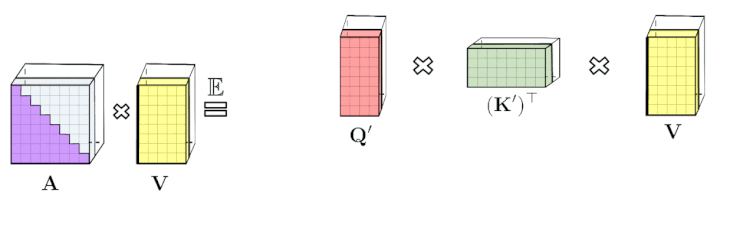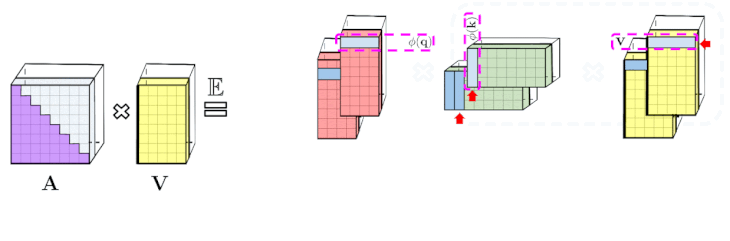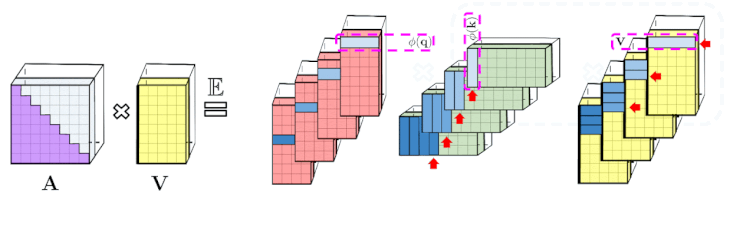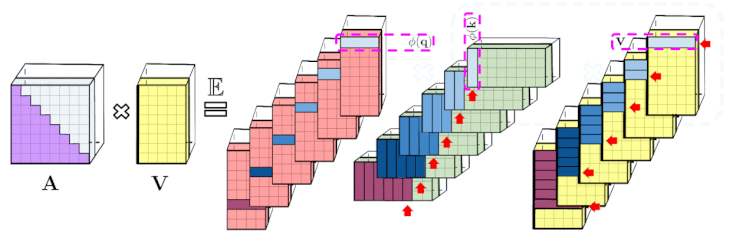
左：標準的な一方向のAttentionでは、下三角部分を取得するためにAttention行列をマスキングする必要があります。
右：左辺の偏りのない近似は、プレフィックス合計メカニズムを介して取得できます。ます、キーと値ベクトルのrandom feature mapsの外積のプレフィックス合計を直接作成します。その後、出行列の新しい行を取得するために、クエリのrandom feature vectorを左に乗算します。