Bi-Tempered Logistic Loss：ノイズの多いデータでニューラルネットをトレーニングするための損失関数(2/3)

１．Bi-Tempered Logistic Loss：ノイズの多いデータでニューラルネットをトレーニングするための損失関数(2/3)まとめ

・バイテンパーは2つのパラメーターを使いロジスティック損失が持つ問題をうまく処理可能
・パラメーターt1は損失関数の有界性、つまり、マージンの最大値を制御する
・パラメーターt2は裾の重さ、つまり、SoftMax関数の減衰の勢いを制御する

２．バイテンパーロジスティック損失とは？

以下、ai.googleblog.comより「Bi-Tempered Logistic Loss for Training Neural Nets with Noisy Data」の意訳です。元記事の投稿は2019年8月26日、Ehsan AmidさんとRohan Anilさんによる投稿です。

直近の論文「Robust Bi-Tempered Logistic Loss Based on Bregman Divergences」では、2つの調整可能なパラメーターによるロジスティック損失を一般化した「バイテンパー(bi-tempered)」を紹介し、これら2つの問題に取り組んでいます。

バイテンパーは、2つの調整可能なパラメーターを使う事で、ロジスティック損失が持つ問題をうまく処理します。私達は、この２つのパラメータを「温度(temperatures)」と呼んでいます。

t1は損失関数の有界性(つまり、マージンの最大値)を表します。
t2は裾の重さ(つまり、伝達関数のテール部の減衰率)を表します
これらのパラメータの性質を以下に示します。

t1とt2の両方を1.0に設定すると、ロジスティック損失関数と同じ動きになります。
t1を1.0未満に設定すると決定境界が狭まります。
t2を1.0より大きい値に設定すると、伝達関数(softmax等)の裾が広くなります。

また、バイテンパー損失を使ったニューラルネットワークトレーニングプロセスを視覚的に確認できるインタラクティブなWebページ「Demo for Bi-Tempered Logistic Loss for Training Neural Nets with Noisy Data」も作成しています。

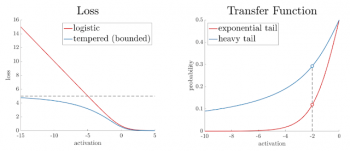
左図：損失関数の有界性。t1が0から1の間にある場合、誤ったラベルが付いた事例が存在しても、各事例で有限量の損失のみが発生します。表示されているグラフはt1 = 0.8のケースです。
右図：伝達関数の裾の重み。t2 => 1.0の場合に、伝達関数のテールに重みが適用され、同じ量の活性化に対してより高い確率を割り当てます。これにより、境界がノイズの多い事例に寄らないようにします。表示されているグラフはt2 = 2.0です。

各温度の効果を実証するために、２つの値を分類する２層のフィードフォワードニューラルネットワークをトレーニングします。このネットワークは、以下の合成データをを分類します。

・円形に配置されたデータ１
・データ１を囲むように同心円に配置されたデータ２

インタラクティブな視覚化を使用して、ブラウザでこれを試すことができます。標準のロジスティック損失関数を使用してみましょう。バイテンパーロジスティック損失で、両方の温度を1.0に設定する事と同じです。

以下に、クリーンなデータセット、マージンの小さいノイズを含むデータセット、マージンの大きいノイズを含むデータセット、およびランダムノイズを含むデータセットに対する各損失関数の効果を示します。

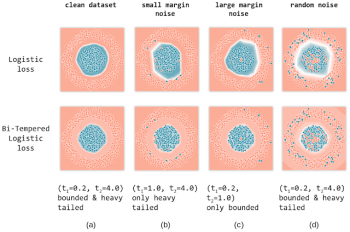
ロジスティック損失とバイテンパーロジスティック損失の対比の図
（a）ノイズのないラベル
（b）マージンの小さいノイズを含むラベル
（c）マージンの大きいノイズを含むラベル
（d）ランダムラベルノイズ。
焼戻し損失(tempered loss)の温度値(t1、t2)が各図の上に示されています。全てのケースにおいて、バイテンパーロジスティック損失関数を使用した学習による決定境界が、ロジスティック損失関数による決定境界よりも優れていることがわかります。