Minerva:大学受験レベルの数学を解答可能な言語モデル(2/2)

１．Minerva:大学受験レベルの数学を解答可能な言語モデル(2/2)まとめ

・Minervaは推論ミスや計算ミスなどまだ相応な間違いをする事がわかっている
・また最終的に正しい答えに到達しても途中の推論に誤りがある場合もある
・モデルが出した答えの正しさを自動的に検証できないという制限もある

２．Minervaの性能

以下、ai.googleblog.comより「Minerva: Solving Quantitative Reasoning Problems with Language Models」の意訳です。元記事は2022年6月30日、Ethan DyerさんとGuy Gur-Ariさんによる投稿です。

アイキャッチのクレジットはPhoto by Roman Lopez on Unsplash

STEMベンチマークによる評価

Minervaの数量的推論能力を検証するために、小学校レベルの問題から大学院レベルのコースワークまで、難易度の高いSTEMベンチマークでモデルを評価しました。

・MATH: 高校数学レベルの問題

・MMLU-STEM: Massive Multitask Language Understanding benchmarkのサブセットで、STEM領域(科学・技術・工学・数学)に焦点を当て、高校、大学レベルのトピックをカバー

・GSM8k: 基本的な算術演算を含む小学生レベルの数学問題で、初等教育レベルで解くことができる問題

また、MIT OpenCourseWareから収集した固体化学、天文学、微分方程式、特殊相対性理論など様々なSTEMトピックをカバーする大学・大学院レベルの問題集OCWCoursesでMinervaを評価しました。

すべてのケースで、Minervaは最先端の結果を得ており、時には大差をつけることもありました。

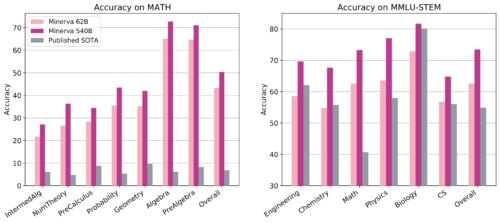
MATHとMMLU-STEMの評価結果。科学・技術・工学・数学の分野をカバーする高校生と大学生レベルの問題を含んでいます。

Model	MATH	MMLU-STEM	OCWCourses	GSM8k
Minerva	0.503	0.75	0.308	0.785
Published state of the art	0.069	0.55	–	0.744

Minerva 5400億は、STEM評価データセットにおいて、従来の最高のスコアを大幅に向上しました。

Minervaがまだ間違える事

Minervaはまだ相応な間違いをします。モデルを改善することができる領域をよりよく特定するために、モデルが間違える問題のサンプルを分析したところ、ほとんどの間違いは簡単に解釈できることがわかりました。約半数は計算ミスで、残りの半数は論理的な思考の連鎖に則っていない推論ミスです。

また、最終的に正しい答えに到達しても、推論に誤りがある場合もあります。私達はこのようなケースを「誤検出」と呼んでおり、これをモデルの総合成績にカウントしてしまっています。私たちの分析では、誤検出の割合は比較的低いことが分かっています。(Minerva 620億のMATHでの誤検出は8％未満)

以下は、モデルが犯す間違いの例です。

計算ミスの事例：式の両辺の平方根を誤って相殺しています

推論ミスの事例：このモデルは、4回目の練習におけるフリースローの回数を計算していますが、この回数を1回目の練習の最終的な答えとして使用しています。

制限事項

私たちの定量的推論へのアプローチは、正式な数学に基づいたものではありません。Minervaは質問を解析し、自然言語とLaTeXの数式を混ぜて答えを生成しますが、その根底にある数学的構造は明らかではありません。

このアプローチには、モデルの答えを自動的に検証することができないという重要な制限があります。最終的な答えが分かっていて検証できる場合でも、モデルは間違った推論ステップを使って正しい最終的な答えに到達することがあり、それは自動的に検出することができません。このような制限は、定理証明用の公式な手法(例えば、Coq、Isabelle、HOL、Lean、Metamath、Mizarを参照のこと)にはありません。一方、非公式な手法の利点は、形式化できないような多様な問題に適用できることです。

今後の方向性

機械学習モデルは多くの科学的分野において印象的なツールとなっていますが、それらはしばしば特定のタスクを解決するための狭い範囲に限定されています。私達は、定量的推論問題を解くことができる汎用的なモデルが、科学と教育のフロンティアを押し広げるのに役立つことを期待しています。

定量的推論が可能なモデルは、研究者のための有用な補助ツールとして、また学生のための新しい学習機会を可能にするなど、多くの応用の可能性があります。その小さな一歩として、Minervaを紹介します。Minervaのデモをもっと見るには、minerva-demo.github.ioより操作可能なサンプルエクスプローラーをご覧ください。

微積分と三角法を使った問題の解答。MATHデータセットからの問題で、円運動をする粒子の速度を問うものです。Minervaは正しいステップバイステップの解答を見つけます。その過程で、Minervaは時間微分を計算し、三角恒等式を適用します。

謝辞

Minervaは、Google Researchの複数のチームにまたがる共同作業でした。共著者のAitor Lewkowycz, Ambrose Slone, Anders Andreassen, Behnam Neyshabur, Cem Anil, David Dohan, Henryk Michalewski, Imanol Schlag, Theo Gutman-Solo, Vedant Misra, Vinay Ramasesh, Yuhuai Wuと、共同研究者のEric Zelikman, Yasaman Razeghiに謝辞を述べたいと思います。また、PaLMチーム、T5Xチーム、Flaxformerチーム、JAXチームにも感謝します。この投稿のアニメーションをデザインしてくれたTom Smallに感謝します。また、Minervaサンプルエクスプローラを開発したVedant Misraに感謝します。