古典的アルゴリズムと量子アルゴリズムを組み合わせて量子モンテカルロ法を実現(2/3)

１．古典的アルゴリズムと量子アルゴリズムを組み合わせて量子モンテカルロ法を実現(2/3)まとめ

・フェルミ粒子には負符号問題というマイナスのエネルギーを持っているように見えるケースがある
・この負符号問題を量子コンピュータと古典的コンピュータを組み合わせて測定できないか挑戦
・モンテカルロ法実行前に量子コンピュータ上で測定を行い古典コンピュータ作業の精度を上げた

２．ハイブリッドモンテカルロ

以下、ai.googleblog.comより「Hybrid Quantum Algorithms for Quantum Monte Carlo」の意訳です。元記事は2022年3月16日、William J. Hugginsさんによる投稿です。

アイキャッチ画像のクレジットはPhoto by Mark de Jong on Unsplash

しかし、化学や材料科学の分野では、この考え方だけでは基底状態(ground state)を見つけることはできません。電子はフェルミ粒子(fermions)と呼ばれる種類の粒子に属し、その振る舞いには量子力学的な驚くべき癖があります。

2つの同じフェルミ粒子が入れ替わると、量子力学的波動関数(フェルミ粒子について知るべきことをすべて教えてくれる数学的記述)はマイナスになります。

このマイナス記号が、有名なパウリの排他原理(Pauli exclusion principle、2つのフェルミ粒子が同じ状態を占めることはできないという事実)を生み出しています。

また、プロジェクターモンテカルロ計算が非効率的になったり、完全に破綻したりすることもあります。

このフェルミ粒子負符号問題を解決するには、モンテカルロ法のアルゴリズムに手を加えて、基底状態の近似値から得られる情報を取り入れるのが一般的です。最低エネルギー状態の近似をガイドとして使用することで、通常、破綻を回避し、真の基底状態の特性を正確に推定することさえ可能です。

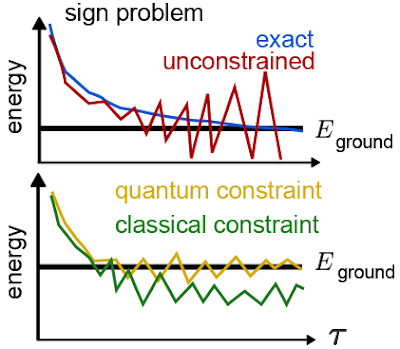
上図：フェルミ粒子負符号問題がどのように現れるかの説明図
青線の曲線に沿うのではなく、赤の曲線に沿うようにマイナスのエネルギーが推定されるため、不安定になります
下図：負符号問題を解決すると、どのように改善されるかの例
量子コンピュータを用いることで、計算の指針となる最初の推測を改善し、より正確な答えを得ることが期待されます

最も難しい問題(化学結合の切断のモデル化など)では、古典コンピュータで十分に正確な初期推測を行うには計算コストがかかりすぎるため、共同研究者のJoonho Lee博士が量子コンピュータが役に立つのではないかと尋ねてきたのです。

私たちはすでに、量子コンピュータを使って量子系の基底状態を近似的に求めることができることを、過去の実験で実証しています。

この実験の初期には、化学反応速度などの物理的性質に直接関連する量(状態のエネルギーなど)を測定することを目的としていました。

この新しいハイブリッドアルゴリズムでは、その代わりに、まったく異なる種類の測定を行う必要がありました。

古典コンピュータでモンテカルロ法を用いて生成された状態と、量子コンピュータで生成された状態が、どの程度離れているかを定量的に測定するのです。

最近開発した技術により、モンテカルロ法を実行する前に、量子コンピュータ上ですべての測定を行うことができ、量子コンピュータ上の作業を古典コンピュータ上の作業から切り離すことができるようになったのです。

私達の計算のイメージ図
量子プロセッサー(右)は、古典的コンピュータ(左)の指針となる情報を測定します。十字は量子ビットを表し、最大の実験時に使われたものは緑色の網掛けになっています。矢印の方向は、量子プロセッサーが古典的コンピュータからのフィードバックを必要としないことを示します。赤い棒は、フェルミ粒子負符号の問題を回避し、基底状態のエネルギーなどの特性を正しく推定するために、量子コンピュータからのデータによってフィルタリングされる古典的計算の部分を示しています。