オームの法則を使って代替経路問題を解く(1/2)

１．オームの法則を使って代替経路問題を解く(1/2)まとめ

・電気の流れの興味深い特性を道路ネットワークの経路問題に応用した事例の紹介
・送信元と送信先の間に代替経路を構築する問題で電気の流れから得たアイデアを利用
・抵抗を区間を横断するのにかかる時間としてグラフニューラルネットワークでモデル化

２．交通状況を電気の流れとしてモデル化

ネットワークの世界では、様々な場面で観測結果を説明できるモデルが存在します。例えば、最短経路計算のような単純なタスクは、明らかにネットワーク経路問題に適用できますが、生物学にも適用できます。例をあげると、粘菌が迷路の中で最短経路を見つける際などです。

また、ブライスのパラドックス(Braess’s Paradox。ネットワークに資源を追加すると、期待とは逆の効果が得られるという観測)は、道路網だけでなく機械や電気系統でも観測できます。例えば、新しい道路を作ると逆に渋滞が増えたり、電気回路に新しい接続を追加すると電圧が上がったりするのです。このような電気回路と他の種類のネットワークとのつながりを利用して、ネットワークの分割や流れの制御など、さまざまなタスクが行われています。

SIGSPATIAL 2021でBest Paper Awardを受賞した論文「Robust Routing Using Electrical Flows」では、電気の流れの興味深い特性を道路ネットワークの経路問題に応用した事例を紹介しています。具体的には、与えられた送信元と送信先の間に複数の代替経路を構築する問題に対して、電気の流れから得たアイデアを利用しています。

代替経路を見つける事は、ユーザーの好みに最も合う経路を見つけたり、堅牢な経路探索、例えば、交通渋滞があっても良い経路を見つけることを保証する経路探索など、多くの場面で重要です。その過程で、電気の流れを道路ネットワークとしてで素早くモデル化する方法についても説明します。

既存の代替経路アプローチ

道路ネットワークにおける代替経路の計算は比較的新しい研究分野であり、ほとんどの技術はペナルティ法(penalty method)とプラトー法(plateau method)の2つの主要手法のどちらかに依存しています。

前者は、最短経路アルゴリズムを実行して代替経路を繰り返し計算し、その後、すでに計算された最短経路に含まれる区間にペナルティを追加して、さらなる探索を促す方法です。

後者では、出発地と目的地から2つの最短経路樹を同時に構築し、両樹に共通する道路部分を特定するために使用します。そして、そのような共通部分(例えば重要な幹線道路であることが予想されます)を、出発地から目的地までの中間地点として扱います。これらを利用すると代替経路を生成できる可能性があります。

ペナルティ法は、高品質な結果(すなわち、平均移動時間、返された代替経路のセットの多様性と堅牢性)をもたらすことが知られていますが、実際には非常に遅いです。一方、プラトー法は、はるかに速いのですが、提案される代替経路は低品質になります。

代替経路問題の代替案：電気の流れ

私達の手法は異なっており「道路ネットワーク上の経路問題は、多くの点で抵抗ネットワーク上の電流の流れに類似している」と仮定しています。電流は多くの異なる経路を通りますが、抵抗の高い経路では弱く、抵抗の低い経路では強くなります。他の条件はすべて同じです。

私達は道路網をグラフと見なし、交差点をノード、道路をエッジとします。そして、この手法ではグラフを電気回路としてモデル化します。エッジを抵抗に置き換え、その抵抗値は道路の通過時間に等しいとします。そして、出発地と目的地に電池を接続し、その2点間に電流を発生させるのです。

ここでは、抵抗を区間を横断するのにかかる時間としてモデル化しています。つまり、長くて混雑している区間は、抵抗が大きいです。直感的に言えば、電流の流れはネットワーク全体に広がりますが、抵抗の低いルート、つまり高速なルートに集中することになります。電流が通る主要な経路を特定することで、起点から目的地までの実行可能な代替案のセットを構築することができます。

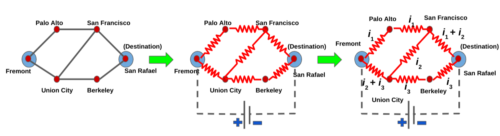
道路網に対応する電気回路の構築例。電流は3つの流れ、i1、i2、i3に分解することができ、それぞれがカリフォルニア州フリーモントからサン・ラファエルへの実行可能な代替経路に相当します。