1.数学的プログラミング:データサイエンス能力を進化させるための大事な習慣(2/3)
・ランダムダーツ投げのような検証は多数の試行が行われるという条件下でのみ有効
・他のモンテカルロ実験と同様に投げた回数が多いほど近似は良くなる
・科学的実験は単なるコーディングを超えた、仮説の探求と検証がなくては終わらない
2.数学的プログラミングの実例
以下、www.kdnuggets.comより「Mathematical programming — Key Habit to Build Up for Advancing Data Science」の意訳です。元記事は2019年5月、Tirthajyoti Sarkarさんによる記事です。
このアイディアはどういう原理なのですか?
このアイディアは非常に単純です。沢山のダーツを投げた場合、ダーツが円の内側に刺さる確率は、正方形の板の面積に対する円の面積の比率になります。
基本的な数学の助けを借りれば、あなたはこの比率がpi / 4である事を示すことができます。 だから、円周率を得るためには、あなたはその数を4倍するだけです。
訳注:一辺の長さをXとすると、正方形の面積はX²、円の面積は半径×半径×pi、つまり(X÷2)×(X÷2)×pi=X²/4×pi。 X²/4×pi÷X²=pi/4
ここで重要なのは、(円の内側に刺さるダーツの割合が)真の確率と等しくなるように、たくさんのダーツを投げることです。
このランダムなダーツ投げによる検証は、多数の試行が行われるという条件下でのみ有効で、これは大数の法則、または頻度主義者による確率の定義(frequentist definition of probability)から来ています。
Python code
Pythonコードを説明するJupyterノートブックは、私のGithubレポジトリ「tirthajyoti/Stats-Maths-with-Python」にあります。 コピーまたはフォークしてください。手順は簡単です。
訳注:Colabの使い方解説ページにも書いてありますが、GithubにホストされているJupyterノートブックファイルはURLを書き換える(https://github.com/をhttps://colab.research.google.com/github/にする)だけで直接Colab上で試す事ができます。今回のファイルであれば、
https://github.com/tirthajyoti/Stats-Maths-with-Python/blob/master/Computing_pi_throwing_dart.ipynb
を
https://colab.research.google.com/github/tirthajyoti/Stats-Maths-with-Python/blob/master/Computing_pi_throwing_dart.ipynb
にするだけです。はぁ~、便利ですね~、凄いなぁ、隔世の感がありますね。
まず、ダーツをランダムに投げた際に刺さった位置をシミュレートする関数を作成します。
def throw_dart():
"""
Simulates the randon throw of a dart. It can land anywhere in the square (uniformly randomly)
"""
# Center point
x,y = 0,0
# Side of the square
a = 2
# Random final landing position of the dart between -a/2 and +a/2 around the center point
position_x = x+a/2*(-1+2*random.random())
position_y = y+a/2*(-1+2*random.random())
次に、刺さった座標が与えられた際にダーツが円の内側に刺さったかどうかを判定する関数を作成します。
def is_within_circle(x,y):
"""
Given the landing coordinate of a dart, determines if it fell inside the circle
"""
# Side of the square
a = 2
distance_from_center = sqrt(x**2+y**2)
if distance_from_center < a/2:
return True
else:
return False
最後に、ダーツを大量に投げた結果をシミュレートする関数を作成し、累積結果からpiの値を計算します。
def compute_pi_throwing_dart(n_throws):
"""
Computes pi by throwing a bunch of darts at the square
"""
n_throws = n_throws
count_inside_circle=0
for i in range(n_throws):
r1,r2=throw_dart()
if is_within_circle(r1,r2):
count_inside_circle+=1
result = 4*(count_inside_circle/n_throws)
しかし、プログラミングをここで終えてはいけません。このプログラムによる近似値がどれほど優れているか、そしてランダムに投げた回数によってどのように変化するかをテストする必要があります。
他のモンテカルロ実験と同様に、投げた回数が多いほど近似は良くなると予想されます。
これがデータサイエンスと分析の中核です。期待される出力を表示する関数を書いて終わるだけでは不十分です。本質的な部分のプログラミングは完了しているかもしれませんが、科学的実験は単なるコーディングを超えた、仮説の探求と検証がなくては終わりません。
さて、この実験を繰り返して何が起こるか見てみましょう。
Computed value of pi by throwing 3 darts is: 2.6666666666666665
Computed value of pi by throwing 10 darts is: 2.0
Computed value of pi by throwing 31 darts is: 3.6129032258064515
Computed value of pi by throwing 100 darts is: 3.2
Computed value of pi by throwing 316 darts is: 2.8987341772151898
Computed value of pi by throwing 1000 darts is: 3.14
Computed value of pi by throwing 3162 darts is: 3.139784946236559
Computed value of pi by throwing 10000 darts is: 3.1168
Computed value of pi by throwing 31622 darts is: 3.147555499335905
Computed value of pi by throwing 100000 darts is: 3.13736
Computed value of pi by throwing 316227 darts is: 3.1471442982414533
Computed value of pi by throwing 1000000 darts is: 3.138552
Computed value of pi by throwing 3162277 darts is: 3.1433476574000316
Computed value of pi by throwing 10000000 darts is: 3.1417096
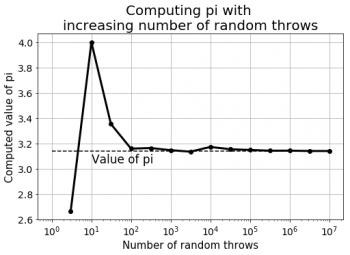
多数のランダムな投擲を繰り返すことで、より良い近似値が得られる事がわかります。
n = 5000000
sum=0
for i in range(20):
p=compute_pi_throwing_dart(n)
sum+=p
print("Experiment number {} done. Computed value: {}".format(i+1,p))
print("-"*75)
pi_computed = round(sum/20,4)
print("Average value from 20 experiments:",pi_computed)
3.数学的プログラミング:データサイエンス能力を進化させるための大事な習慣(2/3)まとめ
1)www.kdnuggets.com
Mathematical programming — Key Habit to Build Up for Advancing Data Science
2)medium.com
Essential Math for Data Science
3)github.com
tirthajyoti/Stats-Maths-with-Python



コメント