超並列グラフ計算：理論から実践へ(1/2)

１．超並列グラフ計算：理論から実践へ(1/2)まとめ

・大規模なグラフは数千億の頂点を含むため一台のコンピュータでは処理しきれない
・複数のコンピューターで分散処理を行う事で兆単位のグラフを処理できるが課題も発生
・分散ハッシュテーブルを使用する事で従来手法より効率的にアルゴリズムを実装できた

２．超並列グラフ計算とは？

以下、ai.googleblog.comより「Massively Parallel Graph Computation: From Theory to Practice」の意訳です。元記事の投稿は2021年3月18日、Jakub ŁąckiさんとVahab Mirrokniさんによる投稿です。

本記事もそうですが、様々な場所で「～の問題をグラフ問題の応用として考えると非常にスムーズに解決する事が出来る」的な表現を見る事があるので、グラフから考える発想は身に着けたいなと思っています。

パラレルなイメージが伝わると良いなと思いながら選んだアイキャッチ画像のクレジットはPhoto by Jonathan Pendleton on Unsplash

グラフは、実体同士の接続を理論的に表現するために有用な手法であり、人気度を元にWebページのランキングを作成したり、ソーシャルネットワーク上の繋がりを表現したり、道案内の支援まで、データサイエンスのさまざまな目的で使用されてきました。多くの場合、このようなアプリケーションでは、数千億の頂点(エッジ)を含むグラフの処理が必要になります。これは、一台の市販コンピュータで処理するには大きすぎます。

グラフアルゴリズムを規模拡大するための一般的なアプローチは、分散して実行することです。つまり、データ(およびアルゴリズム)を複数のコンピューターに分割して、計算を並列に実行します。このアプローチでは、数兆のエッジを持つグラフを処理できますが、新しい課題も発生します。つまり、各コンピューターは一度に入力グラフの小さな部分しか見ることができないため、複数のコンピューターに分割するためにマシン間通信とそのためのアルゴリズムを設計する必要があるのです。

分散アルゴリズムを実装するためのフレームワークであるMapReduceは、2008年に紹介されました。これは、優れた障害耐性機能を提供しながらマシン間の通信を透過的に処理し、Pregel、Apache Hadoopなどの多くの分散計算フレームワークの開発に影響を与えました。それでも、非常に大きなグラフで分散計算を行うためのアルゴリズムを開発するという課題は残っており、連結成分、最大マッチング、最短経路などの基本的な問題に対しても、これらに対処できる効率的なアルゴリズムを設計することが活発な研究分野です。

最近の研究では、連結成分(理論と実践の両方)や階層的クラスタリングのアルゴリズムなど、多くの問題に対する新しいアルゴリズムが実証されていますが、さまざまな問題をより迅速に解決できる方法が依然として必要でした。

本日、この問題に対処する2つの最近の論文を紹介します。最初に分散グラフアルゴリズムの理論モデルを構築する論文、次にモデルをどのように適用できるかを示す論文を示します。

論文「Massively Parallel Computation via Remote Memory Access」で提案されたモデルであるAdaptive Massively Parallel Computation(AMPC)は、MapReduceの理論的機能を強化し、より少ない計算回で多くのグラフ問題を解決するための経路を提供します。

また、AMPCモデルを実際に効果的に実装する方法も示します。最大の独立集合、最大のマッチング、連結成分、最小のスパニングツリーのアルゴリズムを含む、ここで説明する一連のアルゴリズムは、現在の最先端のアプローチよりも最大7倍高速に動作します。

MapReduceの制限
グラフアルゴリズムを開発する際のMapReduceの制限を理解するために、連結成分問題の単純化された変形を検討してください。

入力は根(ルート)を持つツリー構造の集まりであり、目標は各辺(ノード)についてそのルートを計算することです。

この一見単純な問題でさえ、MapReduceで解決するのは簡単ではありません。事実、Massively Parallel Computation(MPC)モデルでは、log nに比例する回数の計算が少なくとも必要であると広く信じられています。ここで、nはグラフ内のノードの総数で、MPCモデルはMapReduce、Pregel、Apache Giraph、およびその他の多くの分散計算フレームワークの背後にある理論モデルです。

log nはそれほど多くないように思われるかもしれませんが、兆単位のエッジを持つグラフを処理するアルゴリズムは、各計算回(ラウンド)で数百テラバイトのデータをディスクに書き込むことが多いため、計算回数を少しでも減らす事は、計算機資源の大幅な節約に繋がります。

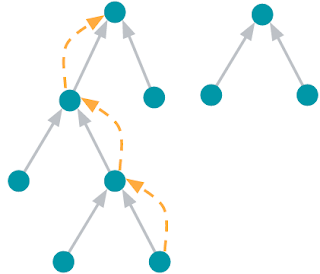
ルートノードを見つける問題。ノードは青い円で表されます。灰色の矢印は、各ノードの親を指しています。ルートノードとは、親のないノードです。オレンジ色の矢印は、アルゴリズムがノードからノードが属するツリーのルートまでたどる道筋を示しています。

同様な問題は、連結成分を見つける問題や階層的クラスタリングを計算するアルゴリズムにも存在しました。

私達は分散ハッシュテーブル(DHT:Distributed Hash Table)を使用してこれらのアルゴリズムを実装することで、MapReduceの制限を回避できる事を発見しました。ここでDHTはキーと値のペアのコレクションで初期化され、提供されたキーに関連付けられた値をリアルタイムで返すサービスとして実装しています。

私達の実装では、ノード毎に、DHTはその親ノードを格納します。次に、グラフノードを処理するマシンは、DHTを使用して、ツリーがルートに到達するまでツリーを「渡り歩く」事ができます。DHTの使用は、この特定の問題に対してはうまく機能しましたが(入力ツリーが深すぎないことに依存していましたが)、このアイデアをより広く適用できるかどうかは不明でした。