1.Dual Mirror Descent:どのタイミングでどのくらい売るのが最も儲かるかを予測する(2/2)まとめ
・資源の制約を扱う際のシンプルで強力なアイデアは「価格」の概念を導入する事
・ミラーディセントは時間の経過とともに一様に資源が消費されるようにすることを目指す
・デュアルミラー降下法はシンプルで仮定が少ないため柔軟で良い成績を収める事が出来る
2.Dual Mirror Descentの特徴
以下、ai.googleblog.comより「Robust Online Allocation with Dual Mirror Descent」の意訳です。元記事の投稿は2022年9月16日、Santiago BalseiroさんとVahab Mirrokniさんによる投稿です。
アイキャッチ画像はstable diffusionによる生成
デュアルミラー降下法で多様な場面でベストスコアを達成
資源の制約を扱う際のシンプルで強力なアイデアは、資源に「価格」を導入することで、意思決定の際にリソースを消費する機会コストを考慮できるようにすることです。
例えば、飛行機の座席を今日売ると、明日売る事はできなくなります。この価格は、アルゴリズムの内部会計システムとして有効です。また、資源制約のある複雑な問題を、より単純な資源制約のない時間帯ごとに1つのみを扱う部分問題として分解することができます。
例えば、広告入札問題では、価格は広告主が1単位の予算を消費する機会費用と捕らえる事ができ、広告主は各オークションを独立した入札問題として扱うことができるようになります。
これにより、オンライン広告の配分問題は、最適な意思決定を可能にする資源価格設定問題として再構成されます。
このアルゴリズムの革新的な点は、機械学習を用いてオンライン上で最適な価格を予測することです。機械学習の予測モデルを学習するための一般的な最適化アルゴリズムであるミラー・ディセント(mirror descent)を用いて、価格を動的に選択するのです。
資源価格は最適化の分野では「双対変数(dual variables)」と呼ばれるため、このアルゴリズムをデュアルミラー降下法(dual mirror descent)と呼んでいます。
このアルゴリズムは、時間的に一様な資源消費が最適であると仮定し、各行動の後に双対変数を更新することで逐次的に動作します。
ある時点(t)で、報酬から資源を消費する機会コストを引いたものを最大化する行動(xt)をとることから始まります。(下の上の灰色のボックスで示されています。)
アクション(例えば、いくらで入札するか、どの広告を表示するか)は、十分な資源が利用可能であれば実行されます。
次に、アルゴリズムは資源消費の誤差(gt)を計算します。これは、時間の経過とともに一様な消費と実際のリソース消費の差です。(下の3番目のグレーのボックスで示します。)
この誤差をもとに、次の時間帯の新しい双対変数がミラー・ディセント法で計算され、次のアクションに反映されます。
ミラー・ディセントは、誤差を限りなくゼロに近づけ、デュアル変数の推定精度を向上させることで、時間の経過とともに一様に資源が消費されるようにすることを目指します。
一様に資源消費という仮定は意外かもしれませんが、好機を逃さないことに役立ち、商業的な目標に合致することが多いので効果的です。ミラー降下法では、様々な更新ルールも可能です。詳細は論文にあります。
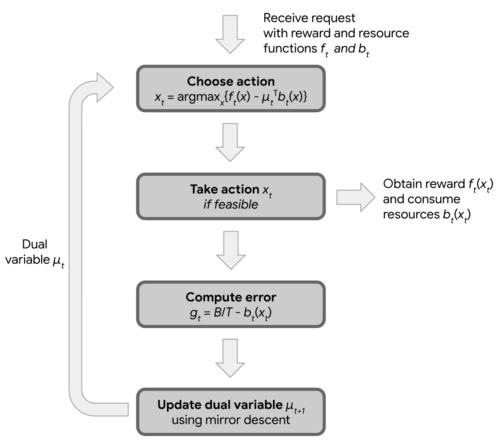
デュアルミラー降下アルゴリズムの概要
設計上、デュアルミラー降下法には自己修正機能があり、資源を早く枯渇させたり、資源消費を長く抑えすぎて好機を逃したりすることを防ぐことができます。ある要求が目標よりも多くの資源を消費したり、少ない資源を消費したりすると、対応する双対変数が増減します。そして、資源の価格が高くなったり低くなったりすると、将来の行動はより保守的または積極的に資源を消費するように選択されます。
このアルゴリズムは実装が容易であり、高速であり、かつ様々な環境下で顕著な性能を発揮します。以下は本アルゴリズムの特徴です。
・既存の手法では、過去のデータを用いて大規模な補助最適化問題を定期的に解く必要がります。これに対し、本アルゴリズムは補助的な最適化問題を解く必要がなく、双対変数の更新ルールも非常にシンプルで、多くの場合、線形時間複雑度で実行することが可能である。したがって、高速な判断を必要とする多くのリアルタイムアプリケーションにとって魅力的です。
・問題の構造に関する要件も最小限です。このような柔軟性により、デュアルミラー降下法は最小限の修正で、異なる分野にわたる多くのアプリケーションを扱うことができます。さらに、私達のアルゴリズムは、異なる目的、制約、または正則化に対応するため、柔軟性があります。正則化を用いることで、意思決定者は経済効率以外の重要な目的、例えば、公平性を含めることができます。
・オンライン割り当て問題に対する既存のアルゴリズムは、敵対的または確率的な入力データのどちらかに合わせて作られています。敵対的入力に対するアルゴリズムは、データの構造についてほとんど仮定しないため堅牢ですが、その代わり、実際には悲観的すぎる性能保証を得る事になります。一方、確率的入力に対するアルゴリズムは、データの統計的パターンを利用することでより良い性能保証を得ることができますが、モデルが誤って指定された場合には性能が低下することがあります。しかし、デュアルミラー降下法は、確率的入力モデルと敵対的入力モデルの両方で、入力モデルの構造を意識することなく、最適に近い性能を達成することができます。同時近似アルゴリズム(simultaneous approximation algorithms)に関する既存の研究と比較して、私達の手法はより汎用的で、幅広い問題に適用でき、予測も不要です。以下は、私達のアルゴリズムと他の最先端手法との比較です。結果は広告配分問題の合成データに基づいています。
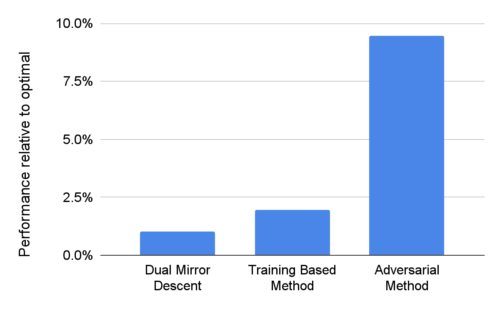
デュアルミラー降下法、トレーニングベース法、敵対的手法の最適オフライン解に対する性能。値が低いほど、最適なオフラインの割り当てに近いパフォーマンスを示します。結果は、広告配分問題の公開データに基づく合成実験により生成されました。
まとめ
この投稿では、オンライン割り当て問題のアルゴリズムとして、シンプルで堅牢かつ柔軟なデュアルミラー降下法を紹介しました。
特に注目すべきは、オンライン割り当てアルゴリズムの長い研究の後、デュアルミラー降下法が、従来の手法と比較して優れた堅牢性優先のアルゴリズムをより幅広く解析する方法を提供することです。
デュアルミラー降下法は、いくつかの商業分野で幅広く応用されており、Googleでは、アルゴリズムの優れた意思決定によって広告主がより多くの価値を獲得できるよう、長期にわたって使用されてきました私達はまた、ミラー・ディセントとPIコントローラとの関連について、さらなる研究を進めています。
謝辞
共著者のHaihao LuとBalu Sivan、そしてKshipra Bhawalkarの多大な支援と貢献に感謝します。また、広告品質チームと市場アルゴリズム研究の共同研究者にも感謝します。
3.Dual Mirror Descent:どのタイミングでどのくらい売るのが最も儲かるかを予測する(2/2)関連リンク
1)ai.googleblog.com
Robust Online Allocation with Dual Mirror Descent
2)arxiv.org
From Online Optimization to PID Controllers: Mirror Descent with Momentum



