1.TensorNetwork:効率的なテンソル計算のためのオープンソースライブラリ(1/2)まとめ
・量子状態など指数関数的に計算が増える難問に取り組む際はテンソルネットワークが使用される事が多い
・テンソルネットワークは機械学習でも使われ始めているが物理学の知識が必要と誤解されている事が多い
・TensorNetworkはテンソルネットワークより広く様々な分野で使いやくするために開発された
2.TensorNetworkとは?
以下、ai.googleblog.comより「Introducing TensorNetwork, an Open Source Library for Efficient Tensor Calculations」の意訳です。元記事のは2019年6月4日、Chase RobertsさんとStefan Leichenauerさんによる投稿です。
高温超伝導体の開発や空間と時間の真の性質の理解など、世界で最も困難な科学的課題の多くは、複雑な量子システムと関わりがあります。
これらの課題を困難にしているのは、量子が取りうる状態が指数関数的に大きくなるため、全ての可能性を計算する事が事実上計算不可能であるということです。
この問題に対処するために、テンソルネットワークと呼ばれるデータ構造が使用されます。
テンソルネットワークは、現実世界の問題に最も関連する量子状態、「低エネルギーの状態(states of low energy)」、に焦点を当て、他の状態を無視します。
テンソルネットワークはまた、機械学習(ML)の分野でも次第に使われるようになってきていますが、MLコミュニティ内での普及を妨げる困難な課題が残っています。
(1)ハードウェアアクセラレータを使用するテンソルネットワークライブラリ製品は、スケーラブルではなく、規模を拡大してテンソルネットワークアルゴリズムを実行する事ができません。
(2)テンソルネットワークの文献のほとんどは物理学の応用問題を対象としており、アルゴリズムを理解するには量子力学の専門知識が必要であるという誤った印象を与えています。
これらの問題に対処するために、私達はTensorNetworkをリリースしています。TensorNetworkはテンソル計算の効率を改善するための、Perimeter Institute for Theoretical PhysicsとX(訳注:旧名Google X、Googleの次世代技術の開発を担う子会社の1つ)と共同開発したものです。
TensorNetworkはバックエンドとしてTensorFlowを使用し、GPU処理用に最適化されています。これにより、CPU上での作業と比較して最大100倍のスピードアップが可能になります。
一連の論文でTensorNetworkを紹介しています。最初の論文「TensorNetwork: A Library for Physics and Machine Learning」では新しいライブラリとそのAPIを紹介し、物理学に馴染のない読者のためにテンソルネットワークの概要を説明します。二つ目の論文「TensorNetwork on TensorFlow: A Spin Chain Application Using Tree Tensor Networks」では、物理学における特定の事例に焦点を当て、GPUを使用する事によって大幅にスピードアップする事を実証します。
Tensor Networkはどのように役立ちますか?
テンソルとは多次元配列であり、次元で分類されます。例えば、ベクトルは1次元テンソル、行列は2次元テンソル、普通の数字はゼロ次元のテンソル(スカラーとも呼ばれます)、などです。
低次テンソルは、明示的に配列またはTijnklm (ijnklmはそれぞれ次数でありインデックスの数を示します)のような数学記号で簡単に表すことができますが、高次テンソルを取り扱う際、この数学的表記法は非常に面倒になります。
その場合、円(または他の形状)に線または足を書き加えるという図表による表記法を使い始めると便利です。足の数はテンソルの次数と同じです。この表記法では、スカラーは単なる円、ベクトルは単一の足、行列は2つの足を持ちます。テンソルのそれぞれの足は、足のサイズで次元を表しています。例えば、空間を通過する物体の速度を表すベクトルは、速度を表すベクトルは、3次元の1次テンソルです。
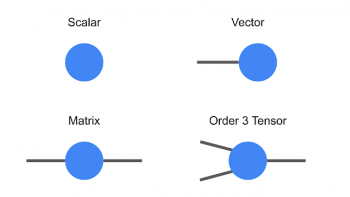
テンソルの図表表記
このようにテンソルを表現することの利点は、数学演算を簡潔に表現出来ることです。たとえば、行列にベクトルを掛けて別のベクトルを作成したり、2つのベクトルを掛けてスカラーを作成したりできます。これらは全て「テンソルの縮約(tensor contraction)」と呼ばれるより一般的な概念の例です。
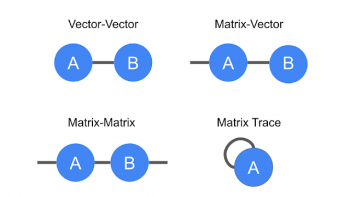
テンソル縮約の図。ベクトルおよび行列の乗算、ならびに行列トレース(行列の対角要素の合計)
以下もテンソルネットワークの簡単な例です。これは、複数のテンソルをテンソル縮約で表現し、新しいテンソルを作り出すグラフィカルな方法です。
各構成テンソルは、それ自身の足の数によって決定される次数を持ちます。ダイアグラムでテンソル同士を繋ぐ辺を形成する接続された足は縮約を表し、残りのどこにも繋がっていない足の数は結果として得られるテンソルの次数を決定します。
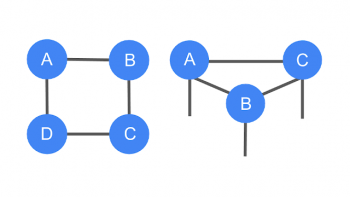
左図:4つの行列の積のトレース、tr(ABCD)。これはスカラーです。未接続の足がないことがわかります。右図:3本の足を持つ3次元テンソルが3本の足が未接続の状態で縮約しています。これは、新しい三次元のテンソルになる事を意味します。
これらの例は非常に単純ですが、テンソルネットワークが扱うテンソルは、様々な方法で縮約された何百ものテンソルになる事がよくあります。
そういった複雑なテンソルを従来の数式的な表記法(Tijnklm )を使って表現すると非常に不明瞭になるでしょう。それが図式的な表記法が1971年にRoger Penroseによって発明された理由です。
3.TensorNetwork:効率的なテンソル計算のためのオープンソースライブラリ(1/2)関連リンク
1)ai.googleblog.com
Introducing TensorNetwork, an Open Source Library for Efficient Tensor Calculations
2)arxiv.org
TensorNetwork: A Library for Physics and Machine Learning
TensorNetwork on TensorFlow: A Spin Chain Application Using Tree Tensor Networks



コメント